Airy Disk Gaussian Fit

Comparing the Airy disk diffraction pattern to its Gaussian approximation

import matplotlib.pyplot as plt
import numpy as np

import mirage as mr
import mirage.vis as mrv

telescope = mr.Telescope(preset='pogs')
telescope.sensor_pixels = np.array([400, 300])
telescope.pixel_scale = 0.005
telescope.fwhm = (
    telescope.airy_disk_fwhm(550) * mr.AstroConstants.rad_to_arcsecond
)  # arcseconds

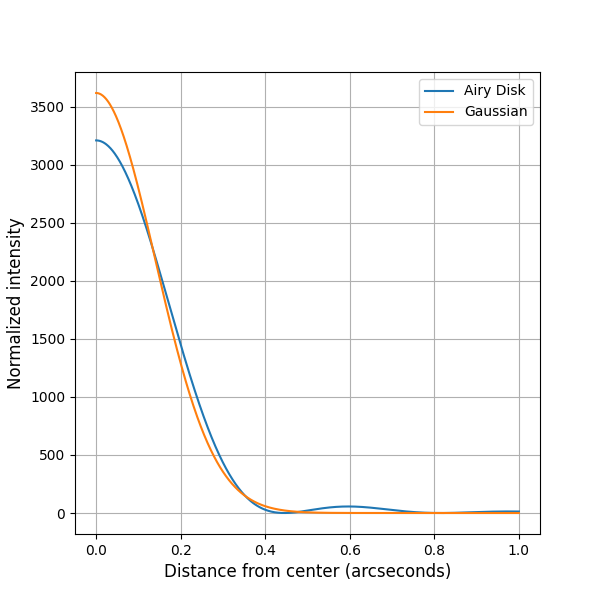
One dimensional falloff as a function of the distance from the center of the image

c_all = 1000
r_pix = np.linspace(0, telescope.sensor_pixels[0] // 2, int(1e3))
theta_arcsec = r_pix * telescope.pixel_scale
theta_rad = mr.dms_to_rad(0, 0, theta_arcsec)
airy_pattern = telescope.airy_disk_pattern(c_all, theta_rad, 550)
gaussian_pattern = telescope.gaussian_diffraction_pattern(c_all, theta_rad)

plt.figure(figsize=(6, 6))
plt.plot(theta_arcsec, airy_pattern, label='Airy Disk')
plt.plot(theta_arcsec, gaussian_pattern, label='Gaussian')
mrv.texit('', 'Distance from center (arcseconds)', 'Normalized intensity')
plt.legend()
plt.show()

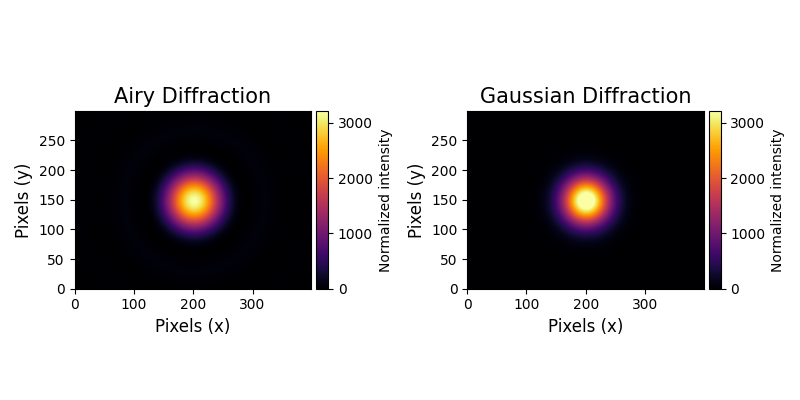
Two dimensional renders

obj_pos = (
    telescope.sensor_pixels[0] // 2 + np.random.rand(),
    telescope.sensor_pixels[1] // 2 + np.random.rand(),
)
x_pix, y_pix = np.meshgrid(
    np.arange(telescope.sensor_pixels[0]), np.arange(telescope.sensor_pixels[1])
)
r_dist = np.sqrt((x_pix - obj_pos[0]) ** 2 + (y_pix - obj_pos[1]) ** 2)
theta_grid_rad = mr.dms_to_rad(0, 0, r_dist * telescope.pixel_scale)

mr.tic()
airy_pattern = telescope.airy_disk_pattern(c_all, theta_grid_rad, 550)
mr.toc()
mr.tic()
gaussian_pattern = telescope.gaussian_diffraction_pattern(c_all, theta_grid_rad)
mr.toc()

Elapsed time: 2.44e-03 seconds
Elapsed time: 5.64e-04 seconds

Let’s look at the volume of both distributions

print(f'Airy disk volume: {np.sum(airy_pattern):.4f}')
print(f'Gaussian volume: {np.sum(gaussian_pattern):.4f}')

Airy disk volume: 20080782.8129
Gaussian volume: 17640682.1520

Visualize the Airy disk on the CCD grid

plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.imshow(
    airy_pattern,
    cmap='inferno',
    extent=[x_pix.min(), x_pix.max(), y_pix.min(), y_pix.max()],
)
mrv.texit('Airy Diffraction', 'Pixels (x)', 'Pixels (y)', grid=False)
plt.colorbar(label='Normalized intensity', cax=mrv.get_cbar_ax())
plt.clim(0, np.max(airy_pattern))
plt.subplot(1, 2, 2)
plt.imshow(
    gaussian_pattern,
    cmap='inferno',
    extent=[x_pix.min(), x_pix.max(), y_pix.min(), y_pix.max()],
)
mrv.texit('Gaussian Diffraction', 'Pixels (x)', 'Pixels (y)', grid=False)
plt.colorbar(label='Normalized intensity', cax=mrv.get_cbar_ax())
plt.clim(0, np.max(airy_pattern))
plt.tight_layout()
plt.show()