Note
Go to the end to download the full example code.
EGI Optimization#
EGI optimization figures recreated in Python, originally published in :cite:p:robinson2022:.
import numpy as np
import pyvista as pv
import scipy.optimize as opt
import mirage as mr
import mirage.vis as mrv
Plotting the EGI of a cube
obj = mr.SpaceObject('cube.obj')
obj.shift_to_center_of_mass()
cpos = [7, 7, 5]
pl = pv.Plotter()
mrv.render_spaceobject(pl, obj, opacity=1, color='linen')
mrv.plot_egi(pl, obj, obj.egi, scale_opacity=False)
pl.camera.position = cpos
pl.show()
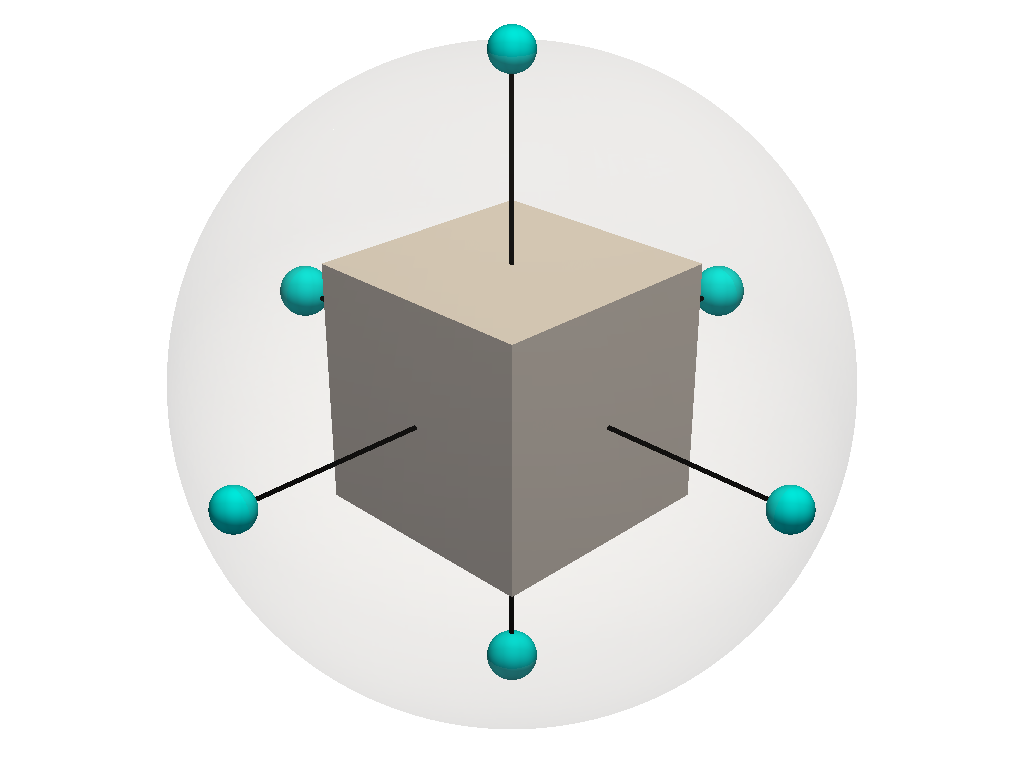
Plotting the initial optimized EGI
n = 500
brdf = mr.Brdf('phong', cd=0.5, cs=0.5, n=10)
normal_candidates = mr.fibonacci_sample_sphere(n)
svb = mr.rand_unit_vectors(n)
ovb = mr.rand_unit_vectors(n)
g_candidates = brdf.compute_reflection_matrix(svb, ovb, normal_candidates)
lc = obj.convex_light_curve(brdf, svb, ovb)
a_candidates = opt.nnls(g_candidates, lc)[0]
valid = a_candidates > np.sum(a_candidates) / 100
egi_candidate = normal_candidates[valid, :] * a_candidates[valid].reshape(-1, 1)
pl = pv.Plotter()
mrv.render_spaceobject(pl, obj, opacity=0.5, color='linen')
mrv.plot_egi(pl, obj, egi_candidate, scale_opacity=True)
pl.camera.position = cpos
pl.show()
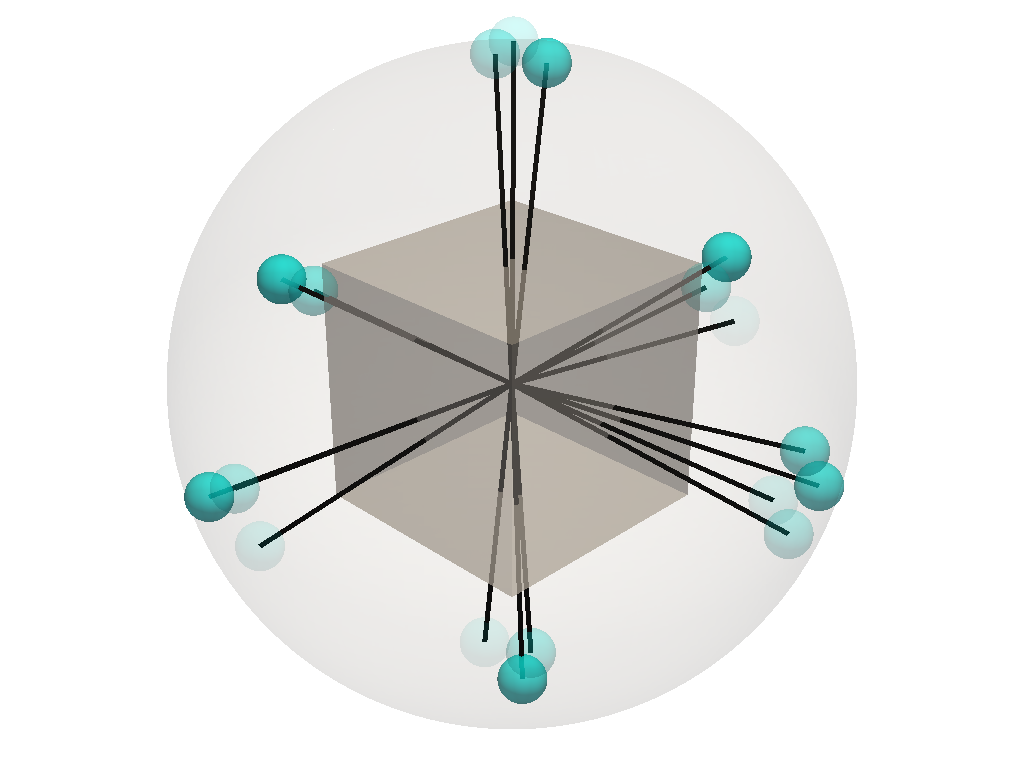
Plotting the resampled EGI
resampled_n_candidates = []
nc = 100
for n_cand in mr.hat(egi_candidate):
resampled_n_candidates.append(mr.rand_cone_vectors(n_cand, np.pi / 20, nc))
resampled_n_candidates = np.vstack(resampled_n_candidates)
g_candidates = brdf.compute_reflection_matrix(svb, ovb, resampled_n_candidates)
lc = obj.convex_light_curve(brdf, svb, ovb)
a_candidates = opt.nnls(g_candidates, lc)[0]
valid = a_candidates > np.sum(a_candidates) / 100
egi_candidate_resampled = resampled_n_candidates[valid, :] * a_candidates[
valid
].reshape(-1, 1)
pl = pv.Plotter()
mrv.render_spaceobject(pl, obj, color='linen', opacity=0.5)
mrv.scatter3(pl, 1.2 * resampled_n_candidates, color='r', point_size=3, opacity=0.5)
mrv.plot_egi(pl, obj, egi_candidate_resampled, scale_opacity=True)
pl.camera.position = cpos
pl.show()
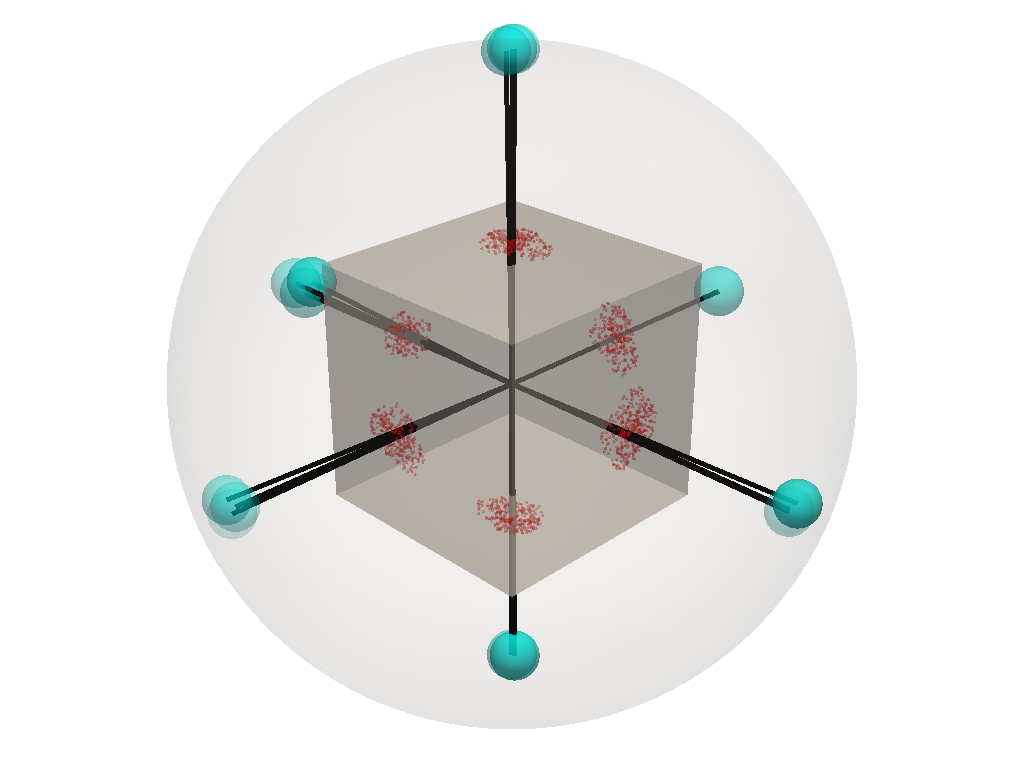
Plotting merged EGI
egi_merged = mr.merge_clusters(egi_candidate_resampled, np.pi / 10)
pl = pv.Plotter()
mrv.render_spaceobject(pl, obj, color='linen', opacity=0.5)
mrv.plot_egi(pl, obj, egi_merged)
pl.camera.position = cpos
pl.show()
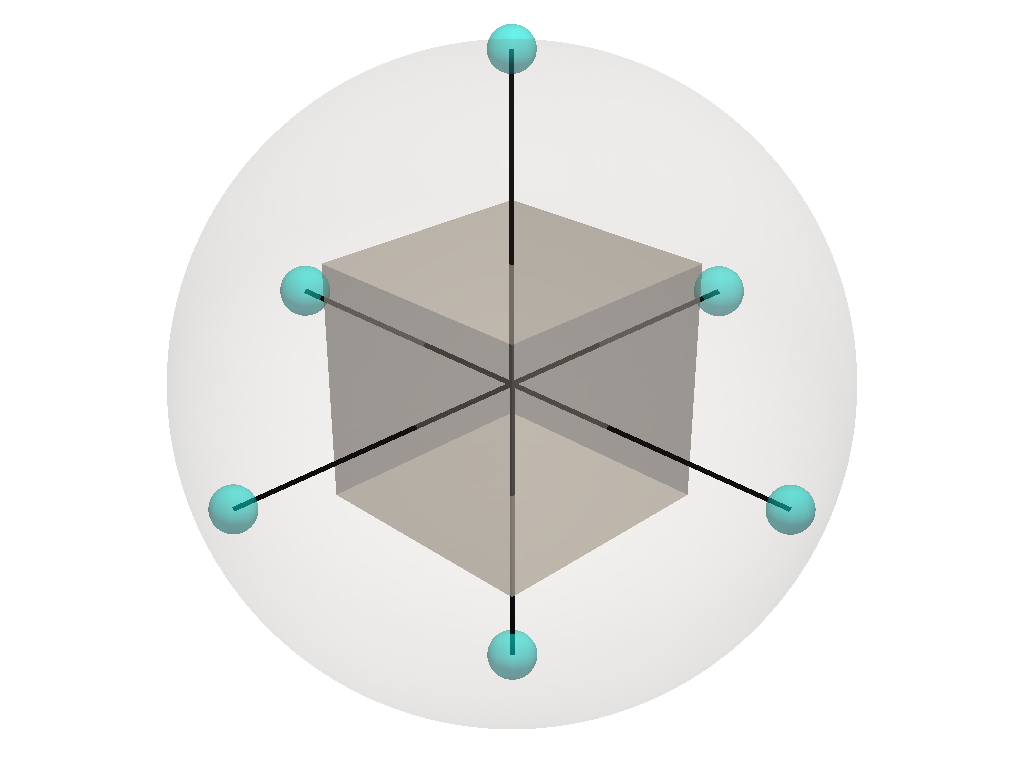
Plotting the reconstructed object
egi_merged -= np.sum(egi_merged, axis=0) / egi_merged.shape[0]
mr.tic()
# obj_reconstructed = mr.construct_mesh_from_egi(egi_merged)
h = mr.optimize_supports_little(egi_merged)
dt = mr.toc(return_elapsed_seconds=True)
obj_reconstructed = mr.construct_from_egi_and_supports(egi_merged, h)
obj_reconstructed.shift_to_center_of_mass()
pl = pv.Plotter(shape=(1, 2), window_size=(1000, 500))
pl.subplot(0, 0)
mrv.render_spaceobject(pl, obj, opacity=1, color='linen')
pl.add_text('Original', font='courier', position='upper_left')
pl.subplot(0, 1)
mrv.render_spaceobject(pl, obj_reconstructed, opacity=1, color='linen')
pl.add_text('Reconstructed', font='courier', position='upper_left')
pl.link_views()
pl.camera.position = cpos
pl.camera.zoom(1.4)
pl.show()
| niter |f evals|CG iter| obj func |tr radius | opt | c viol | penalty |barrier param|CG stop|
|-------|-------|-------|-------------|----------|----------|----------|----------|-------------|-------|
| 1 | 1 | 0 | +1.0000e+00 | 1.00e+00 | 4.67e-02 | 9.99e-01 | 1.00e+00 | 1.00e-01 | 0 |
/Users/liamrobinson/Documents/maintained-research/mirage/.venv/lib/python3.12/site-packages/scipy/optimize/_differentiable_functions.py:316: UserWarning: delta_grad == 0.0. Check if the approximated function is linear. If the function is linear better results can be obtained by defining the Hessian as zero instead of using quasi-Newton approximations.
self.H.update(self.x - self.x_prev, self.g - self.g_prev)
| 2 | 2 | 1 | +6.4029e+00 | 5.65e+00 | 1.71e-01 | 8.38e-01 | 8.55e+00 | 1.00e-01 | 4 |
| 3 | 3 | 3 | +6.4029e+00 | 5.65e-01 | 1.71e-01 | 8.38e-01 | 8.55e+00 | 1.00e-01 | 4 |
| 4 | 4 | 5 | +1.0214e+01 | 3.19e+00 | 1.62e-02 | 3.32e-01 | 1.33e+02 | 1.00e-01 | 4 |
| 5 | 5 | 6 | +1.1901e+01 | 4.89e+00 | 2.91e-03 | 5.77e-02 | 1.33e+02 | 1.00e-01 | 4 |
| 6 | 5 | 6 | +1.1901e+01 | 2.45e+01 | 2.58e-03 | 5.77e-02 | 1.00e+00 | 2.00e-02 | 0 |
| 7 | 6 | 7 | +1.1685e+01 | 2.45e+01 | 2.72e-03 | 1.04e-03 | 1.00e+00 | 2.00e-02 | 4 |
`gtol` termination condition is satisfied.
Number of iterations: 7, function evaluations: 6, CG iterations: 7, optimality: 2.72e-03, constraint violation: 1.04e-03, execution time: 0.029 s.
Reconstructing with the non-sparse EGI
pl = pv.Plotter(shape=(1, 4), window_size=(2000, 500))
pl.subplot(0, 0)
mrv.render_spaceobject(pl, obj, opacity=1, color='linen')
pl.add_text('Truth', font='courier', position='upper_left')
egi_candidate = mr.close_egi(egi_candidate)
egi_candidate_resampled = mr.close_egi(egi_candidate_resampled)
pl.subplot(0, 1)
mr.tic()
# obj_reconstructed_initial = mr.construct_mesh_from_egi(egi_candidate)
h_initial = mr.optimize_supports_little(egi_candidate)
dt_initial = mr.toc(return_elapsed_seconds=True)
obj_reconstructed_initial = mr.construct_from_egi_and_supports(egi_candidate, h_initial)
obj_reconstructed_initial.shift_to_center_of_mass()
mrv.render_spaceobject(
pl,
obj_reconstructed_initial,
opacity=0.7,
color='linen',
feature_edges=True,
feature_edge_color='k',
feature_edge_angle=2,
)
mrv.render_spaceobject(pl, obj, style='wireframe', feature_edges=True)
pl.add_text(f'Initial EGI: {dt_initial:.2f}s', font='courier', position='upper_left')
pl.subplot(0, 2)
mr.tic()
h_resampled = mr.optimize_supports_little(egi_candidate_resampled)
# obj_reconstructed_resampled = mr.construct_mesh_from_egi(egi_candidate_resampled)
dt_resampled = mr.toc(return_elapsed_seconds=True)
obj_reconstructed_resampled = mr.construct_from_egi_and_supports(
egi_candidate_resampled, h_resampled
)
obj_reconstructed_resampled.shift_to_center_of_mass()
mrv.render_spaceobject(
pl,
obj_reconstructed_resampled,
opacity=0.7,
color='linen',
feature_edges=True,
feature_edge_color='k',
feature_edge_angle=2,
)
mrv.render_spaceobject(pl, obj, style='wireframe', feature_edges=True)
pl.add_text(
f'Resampled EGI: {dt_resampled:.2f}s', font='courier', position='upper_left'
)
pl.subplot(0, 3)
mrv.render_spaceobject(
pl,
obj_reconstructed,
opacity=0.7,
color='linen',
feature_edges=True,
feature_edge_color='k',
feature_edge_angle=2,
)
mrv.render_spaceobject(pl, obj, style='wireframe', color='k', feature_edges=True)
pl.add_text(f'Merged EGI: {dt:.2f}s', font='courier', position='upper_left')
pl.show()

| niter |f evals|CG iter| obj func |tr radius | opt | c viol | penalty |barrier param|CG stop|
|-------|-------|-------|-------------|----------|----------|----------|----------|-------------|-------|
| 1 | 1 | 0 | +1.0000e+00 | 1.00e+00 | 5.70e-01 | 1.00e+00 | 1.00e+00 | 1.00e-01 | 0 |
/Users/liamrobinson/Documents/maintained-research/mirage/.venv/lib/python3.12/site-packages/scipy/optimize/_differentiable_functions.py:316: UserWarning: delta_grad == 0.0. Check if the approximated function is linear. If the function is linear better results can be obtained by defining the Hessian as zero instead of using quasi-Newton approximations.
self.H.update(self.x - self.x_prev, self.g - self.g_prev)
| 2 | 2 | 1 | +2.8452e+00 | 7.00e+00 | 5.91e-01 | 9.99e-01 | 3.55e+00 | 1.00e-01 | 2 |
| 3 | 3 | 3 | +2.8452e+00 | 1.23e+00 | 5.91e-01 | 9.99e-01 | 3.55e+00 | 1.00e-01 | 2 |
| 4 | 4 | 6 | +5.2704e+00 | 8.62e+00 | 6.51e-01 | 9.67e-01 | 8.31e+00 | 1.00e-01 | 2 |
| 5 | 5 | 8 | +5.2704e+00 | 4.31e+00 | 6.51e-01 | 9.67e-01 | 8.31e+00 | 1.00e-01 | 2 |
| 6 | 6 | 10 | +1.9879e+01 | 3.02e+01 | 9.25e-01 | 4.75e-02 | 7.52e+01 | 1.00e-01 | 2 |
| 7 | 7 | 15 | +1.8426e+01 | 3.02e+01 | 8.58e-01 | 1.69e-02 | 7.52e+01 | 1.00e-01 | 4 |
| 8 | 9 | 22 | +1.8426e+01 | 3.02e+00 | 8.58e-01 | 1.69e-02 | 7.52e+01 | 1.00e-01 | 4 |
| 9 | 11 | 30 | +1.6332e+01 | 7.33e+00 | 7.73e-01 | 6.74e-03 | 7.52e+01 | 1.00e-01 | 4 |
| 10 | 13 | 36 | +1.6332e+01 | 7.33e-01 | 7.73e-01 | 6.74e-03 | 7.52e+01 | 1.00e-01 | 4 |
| 11 | 15 | 38 | +1.6332e+01 | 8.50e-02 | 7.73e-01 | 6.74e-03 | 7.52e+01 | 1.00e-01 | 2 |
| 12 | 16 | 39 | +1.6133e+01 | 1.70e-01 | 7.58e-01 | 1.55e-03 | 7.52e+01 | 1.00e-01 | 2 |
| 13 | 18 | 40 | +1.5749e+01 | 1.19e+00 | 7.25e-01 | 5.74e-04 | 7.52e+01 | 1.00e-01 | 2 |
| 14 | 20 | 45 | +1.5749e+01 | 1.56e-01 | 7.25e-01 | 5.74e-04 | 7.52e+01 | 1.00e-01 | 2 |
| 15 | 21 | 47 | +1.5419e+01 | 3.13e-01 | 6.90e-01 | 3.66e-03 | 7.52e+01 | 1.00e-01 | 2 |
| 16 | 22 | 48 | +1.4808e+01 | 6.26e-01 | 6.12e-01 | 6.22e-03 | 7.52e+01 | 1.00e-01 | 2 |
| 17 | 24 | 49 | +1.3783e+01 | 1.25e+00 | 4.34e-01 | 8.92e-03 | 7.52e+01 | 1.00e-01 | 2 |
| 18 | 26 | 54 | +1.3350e+01 | 1.25e+00 | 4.58e-01 | 1.15e-02 | 7.52e+01 | 1.00e-01 | 4 |
| 19 | 28 | 61 | +1.3350e+01 | 1.25e-01 | 4.58e-01 | 1.15e-02 | 7.52e+01 | 1.00e-01 | 4 |
| 20 | 29 | 62 | +1.3159e+01 | 1.25e-01 | 2.88e-01 | 1.16e-02 | 7.52e+01 | 1.00e-01 | 2 |
| 21 | 30 | 63 | +1.3039e+01 | 1.25e-01 | 2.61e-01 | 9.79e-03 | 7.52e+01 | 1.00e-01 | 2 |
| 22 | 31 | 64 | +1.2956e+01 | 2.50e-01 | 1.12e-01 | 6.51e-03 | 7.52e+01 | 1.00e-01 | 2 |
| 23 | 33 | 67 | +1.2951e+01 | 9.38e-01 | 1.28e-01 | 5.68e-04 | 7.52e+01 | 1.00e-01 | 4 |
| 24 | 35 | 71 | +1.2951e+01 | 9.38e-02 | 1.28e-01 | 5.68e-04 | 7.52e+01 | 1.00e-01 | 4 |
| 25 | 37 | 74 | +1.2934e+01 | 1.88e-01 | 5.74e-02 | 1.98e-04 | 7.52e+01 | 1.00e-01 | 2 |
| 26 | 39 | 77 | +1.2930e+01 | 1.88e-01 | 5.79e-02 | 6.37e-05 | 7.52e+01 | 1.00e-01 | 4 |
| 27 | 41 | 81 | +1.2930e+01 | 1.88e-01 | 6.91e-02 | 1.33e-06 | 7.52e+01 | 1.00e-01 | 4 |
| 28 | 43 | 86 | +1.2930e+01 | 1.88e-02 | 6.91e-02 | 1.33e-06 | 7.52e+01 | 1.00e-01 | 4 |
| 29 | 45 | 87 | +1.2927e+01 | 1.31e-01 | 4.57e-02 | 1.68e-08 | 7.52e+01 | 1.00e-01 | 2 |
| 30 | 45 | 87 | +1.2927e+01 | 1.00e+00 | 5.44e-02 | 1.68e-08 | 1.00e+00 | 2.00e-02 | 0 |
| 31 | 46 | 91 | +1.2917e+01 | 1.00e+00 | 3.75e-02 | 1.23e-03 | 1.00e+00 | 2.00e-02 | 4 |
| 32 | 47 | 95 | +1.2918e+01 | 1.00e+00 | 1.94e-02 | 2.97e-04 | 3.69e+00 | 2.00e-02 | 4 |
| 33 | 48 | 99 | +1.2917e+01 | 1.00e+00 | 7.08e-03 | 1.81e-04 | 3.69e+00 | 2.00e-02 | 4 |
`gtol` termination condition is satisfied.
Number of iterations: 33, function evaluations: 48, CG iterations: 99, optimality: 7.08e-03, constraint violation: 1.81e-04, execution time: 0.64 s.
| niter |f evals|CG iter| obj func |tr radius | opt | c viol | penalty |barrier param|CG stop|
|-------|-------|-------|-------------|----------|----------|----------|----------|-------------|-------|
| 1 | 1 | 0 | +1.0000e+00 | 1.00e+00 | 1.26e+00 | 9.99e-01 | 1.00e+00 | 1.00e-01 | 0 |
| 2 | 2 | 1 | +2.1426e+00 | 7.00e+00 | 1.20e+00 | 9.95e-01 | 2.74e+00 | 1.00e-01 | 2 |
| 3 | 3 | 4 | +1.1293e+01 | 2.10e+01 | 1.55e+00 | 8.39e-01 | 1.00e+03 | 1.00e-01 | 4 |
| 4 | 4 | 12 | +5.8985e+01 | 9.54e+01 | 3.44e+00 | 9.93e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 5 | 5 | 19 | +5.4950e+01 | 9.54e+01 | 3.40e+00 | 4.61e-04 | 1.00e+03 | 1.00e-01 | 4 |
| 6 | 7 | 26 | +5.4950e+01 | 9.54e+00 | 3.40e+00 | 4.61e-04 | 1.00e+03 | 1.00e-01 | 4 |
| 7 | 9 | 33 | +5.4950e+01 | 9.54e-01 | 3.40e+00 | 4.61e-04 | 1.00e+03 | 1.00e-01 | 4 |
| 8 | 10 | 36 | +4.9614e+01 | 6.68e+00 | 3.34e+00 | 3.15e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 9 | 12 | 46 | +4.9614e+01 | 6.68e-01 | 3.34e+00 | 3.15e-04 | 1.00e+03 | 1.00e-01 | 4 |
| 10 | 14 | 48 | +4.9614e+01 | 6.68e-02 | 3.34e+00 | 3.15e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 11 | 15 | 50 | +4.9215e+01 | 4.67e-01 | 3.33e+00 | 2.20e-07 | 1.00e+03 | 1.00e-01 | 2 |
| 12 | 16 | 52 | +4.6572e+01 | 9.35e-01 | 3.29e+00 | 1.49e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 13 | 18 | 53 | +4.6572e+01 | 9.35e-02 | 3.29e+00 | 1.49e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 14 | 20 | 54 | +4.6037e+01 | 9.35e-02 | 3.28e+00 | 1.69e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 15 | 21 | 55 | +4.5505e+01 | 6.54e-01 | 3.26e+00 | 5.62e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 16 | 22 | 56 | +4.1772e+01 | 6.54e-01 | 3.14e+00 | 3.00e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 17 | 23 | 57 | +3.8094e+01 | 1.31e+00 | 2.96e+00 | 2.58e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 18 | 25 | 58 | +3.0932e+01 | 2.62e+00 | 2.78e+00 | 4.83e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 19 | 27 | 59 | +3.0932e+01 | 2.62e-01 | 2.78e+00 | 4.83e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 20 | 28 | 60 | +2.9589e+01 | 2.62e-01 | 2.74e+00 | 5.35e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 21 | 30 | 61 | +2.8318e+01 | 5.23e-01 | 2.70e+00 | 1.17e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 22 | 32 | 62 | +2.5949e+01 | 1.05e+00 | 2.58e+00 | 2.37e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 23 | 34 | 63 | +2.5949e+01 | 1.05e-01 | 2.58e+00 | 2.37e-03 | 1.00e+03 | 1.00e-01 | 2 |
| 24 | 35 | 64 | +2.5505e+01 | 7.33e-01 | 2.55e+00 | 2.68e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 25 | 37 | 65 | +2.5505e+01 | 7.33e-02 | 2.55e+00 | 2.68e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 26 | 38 | 66 | +2.5193e+01 | 1.47e-01 | 2.53e+00 | 1.06e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 27 | 40 | 67 | +2.5193e+01 | 2.31e-02 | 2.53e+00 | 1.06e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 28 | 41 | 68 | +2.5095e+01 | 1.62e-01 | 2.52e+00 | 1.05e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 29 | 43 | 69 | +2.5095e+01 | 1.62e-02 | 2.52e+00 | 1.05e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 30 | 44 | 70 | +2.5027e+01 | 3.24e-02 | 2.52e+00 | 2.12e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 31 | 46 | 71 | +2.4891e+01 | 2.27e-01 | 2.51e+00 | 1.55e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 32 | 48 | 72 | +2.4891e+01 | 4.78e-02 | 2.51e+00 | 1.55e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 33 | 49 | 73 | +2.4691e+01 | 4.78e-02 | 2.49e+00 | 1.98e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 34 | 50 | 74 | +2.4493e+01 | 9.57e-02 | 2.48e+00 | 6.56e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 35 | 51 | 75 | +2.4097e+01 | 1.91e-01 | 2.44e+00 | 1.46e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 36 | 53 | 76 | +2.3314e+01 | 1.34e+00 | 2.37e+00 | 9.79e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 37 | 55 | 77 | +2.3314e+01 | 1.34e-01 | 2.37e+00 | 9.79e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 38 | 57 | 78 | +2.3314e+01 | 1.89e-02 | 2.37e+00 | 9.79e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 39 | 58 | 79 | +2.3237e+01 | 3.78e-02 | 2.36e+00 | 6.31e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 40 | 59 | 80 | +2.3083e+01 | 3.78e-02 | 2.35e+00 | 1.86e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 41 | 60 | 81 | +2.2931e+01 | 2.65e-01 | 2.33e+00 | 1.36e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 42 | 61 | 82 | +2.1867e+01 | 5.30e-01 | 2.21e+00 | 6.09e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 43 | 63 | 83 | +1.9798e+01 | 3.71e+00 | 1.90e+00 | 3.19e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 44 | 64 | 95 | +1.9798e+01 | 3.71e-01 | 1.90e+00 | 3.19e-04 | 1.00e+03 | 1.00e-01 | 4 |
| 45 | 66 | 96 | +1.9798e+01 | 3.71e-02 | 1.90e+00 | 3.19e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 46 | 67 | 97 | +1.9658e+01 | 2.60e-01 | 1.87e+00 | 4.64e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 47 | 69 | 98 | +1.9658e+01 | 2.60e-02 | 1.87e+00 | 4.64e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 48 | 70 | 99 | +1.9561e+01 | 5.19e-02 | 1.86e+00 | 9.39e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 49 | 71 | 100 | +1.9370e+01 | 1.04e-01 | 1.82e+00 | 1.29e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 50 | 72 | 101 | +1.8990e+01 | 2.08e-01 | 1.75e+00 | 2.61e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 51 | 74 | 102 | +1.8246e+01 | 2.08e-01 | 1.71e+00 | 9.69e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 52 | 76 | 103 | +1.8246e+01 | 2.08e-02 | 1.71e+00 | 9.69e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 53 | 78 | 104 | +1.8174e+01 | 4.15e-02 | 1.70e+00 | 1.30e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 54 | 80 | 105 | +1.8030e+01 | 2.91e-01 | 1.70e+00 | 2.15e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 55 | 82 | 106 | +1.8030e+01 | 2.91e-02 | 1.70e+00 | 2.15e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 56 | 83 | 107 | +1.7929e+01 | 5.81e-02 | 1.69e+00 | 2.90e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 57 | 84 | 108 | +1.7728e+01 | 4.07e-01 | 1.68e+00 | 1.65e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 58 | 86 | 109 | +1.7728e+01 | 4.07e-02 | 1.68e+00 | 1.65e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 59 | 87 | 110 | +1.7588e+01 | 2.85e-01 | 1.67e+00 | 1.64e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 60 | 89 | 111 | +1.7588e+01 | 2.85e-02 | 1.67e+00 | 1.64e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 61 | 90 | 112 | +1.7491e+01 | 1.99e-01 | 1.67e+00 | 9.88e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 62 | 92 | 113 | +1.7491e+01 | 1.99e-02 | 1.67e+00 | 9.88e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 63 | 93 | 114 | +1.7424e+01 | 1.40e-01 | 1.66e+00 | 5.14e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 64 | 95 | 115 | +1.7424e+01 | 1.40e-02 | 1.66e+00 | 5.14e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 65 | 96 | 116 | +1.7376e+01 | 9.77e-02 | 1.66e+00 | 2.52e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 66 | 98 | 117 | +1.7376e+01 | 9.77e-03 | 1.66e+00 | 2.52e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 67 | 99 | 118 | +1.7344e+01 | 6.84e-02 | 1.66e+00 | 1.22e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 68 | 101 | 119 | +1.7344e+01 | 6.84e-03 | 1.66e+00 | 1.22e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 69 | 102 | 120 | +1.7321e+01 | 4.79e-02 | 1.66e+00 | 5.85e-07 | 1.00e+03 | 1.00e-01 | 2 |
| 70 | 104 | 121 | +1.7163e+01 | 9.57e-02 | 1.65e+00 | 6.20e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 71 | 106 | 122 | +1.7163e+01 | 9.57e-03 | 1.65e+00 | 6.20e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 72 | 108 | 123 | +1.7135e+01 | 6.70e-02 | 1.65e+00 | 1.87e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 73 | 110 | 124 | +1.7135e+01 | 6.70e-03 | 1.65e+00 | 1.87e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 74 | 112 | 125 | +1.7115e+01 | 4.69e-02 | 1.65e+00 | 6.36e-08 | 1.00e+03 | 1.00e-01 | 2 |
| 75 | 114 | 126 | +1.6989e+01 | 9.38e-02 | 1.63e+00 | 3.75e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 76 | 116 | 127 | +1.6745e+01 | 1.88e-01 | 1.61e+00 | 1.61e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 77 | 118 | 128 | +1.6745e+01 | 1.88e-02 | 1.61e+00 | 1.61e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 78 | 120 | 129 | +1.6694e+01 | 1.31e-01 | 1.60e+00 | 1.71e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 79 | 122 | 130 | +1.6694e+01 | 1.31e-02 | 1.60e+00 | 1.71e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 80 | 124 | 131 | +1.6659e+01 | 9.20e-02 | 1.60e+00 | 2.52e-06 | 1.00e+03 | 1.00e-01 | 2 |
| 81 | 126 | 132 | +1.6420e+01 | 6.44e-01 | 1.57e+00 | 1.89e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 82 | 128 | 134 | +1.6420e+01 | 6.44e-02 | 1.57e+00 | 1.89e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 83 | 130 | 135 | +1.6420e+01 | 6.44e-03 | 1.57e+00 | 1.89e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 84 | 131 | 136 | +1.6404e+01 | 6.44e-03 | 1.57e+00 | 3.17e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 85 | 132 | 137 | +1.6387e+01 | 1.29e-02 | 1.57e+00 | 1.05e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 86 | 133 | 138 | +1.6354e+01 | 2.57e-02 | 1.57e+00 | 1.48e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 87 | 134 | 139 | +1.6288e+01 | 5.15e-02 | 1.56e+00 | 1.00e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 88 | 135 | 140 | +1.6157e+01 | 1.03e-01 | 1.54e+00 | 3.59e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 89 | 136 | 141 | +1.5896e+01 | 2.06e-01 | 1.51e+00 | 1.87e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 90 | 138 | 142 | +1.5896e+01 | 2.07e-02 | 1.51e+00 | 1.87e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 91 | 139 | 143 | +1.5844e+01 | 4.14e-02 | 1.50e+00 | 7.40e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 92 | 140 | 144 | +1.5742e+01 | 8.29e-02 | 1.49e+00 | 5.67e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 93 | 142 | 145 | +1.5538e+01 | 1.66e-01 | 1.46e+00 | 4.77e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 94 | 144 | 146 | +1.5538e+01 | 1.66e-02 | 1.46e+00 | 4.77e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 95 | 146 | 147 | +1.5499e+01 | 3.32e-02 | 1.45e+00 | 2.06e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 96 | 147 | 148 | +1.5418e+01 | 3.32e-02 | 1.44e+00 | 9.19e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 97 | 148 | 149 | +1.5338e+01 | 3.32e-02 | 1.43e+00 | 1.67e-04 | 1.00e+03 | 1.00e-01 | 2 |
| 98 | 150 | 150 | +1.5259e+01 | 2.32e-01 | 1.41e+00 | 1.95e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 99 | 152 | 151 | +1.5259e+01 | 2.32e-02 | 1.41e+00 | 1.95e-05 | 1.00e+03 | 1.00e-01 | 2 |
| 100 | 154 | 152 | +1.5205e+01 | 4.64e-02 | 1.40e+00 | 1.25e-05 | 1.00e+03 | 1.00e-01 | 2 |
The maximum number of function evaluations is exceeded.
Number of iterations: 100, function evaluations: 154, CG iterations: 152, optimality: 1.40e+00, constraint violation: 1.25e-05, execution time: 1.5 s.
Total running time of the script: (0 minutes 3.693 seconds)
