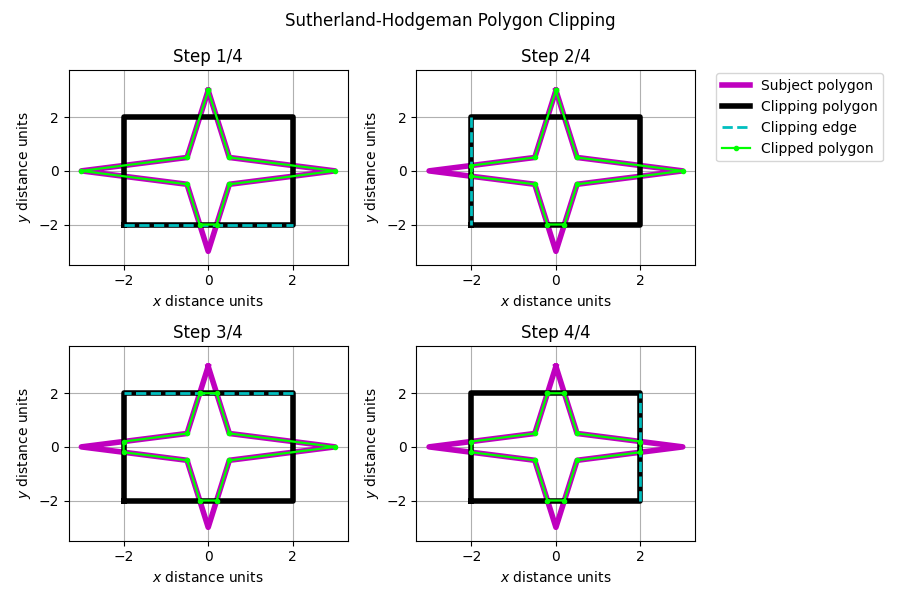
Sutherland-Hodgeman Clipping Algorithm

[Taichi] version 1.7.2, llvm 15.0.7, commit 0131dce9, osx, python 3.11.10
[Taichi] Starting on arch=arm64

from itertools import cycle

import matplotlib.pyplot as plt
import numpy as np
import pyvista as pv
import taichi as ti
from matplotlib.patches import Polygon


def plot_poly(edges: np.ndarray, **kwargs) -> None:
    edges = np.array(edges)
    t = np.array(list(edge_iterator(edges)))
    edges = np.vstack((t[:, 0, :], t[0, 0, :]))
    plt.gca().add_patch(Polygon(edges, facecolor='None'))
    plt.plot(edges[:, 0], edges[:, 1], **kwargs)


def edge_iterator(edges: np.ndarray) -> np.ndarray:
    c = cycle(edges)
    current = None
    for i in range(edges.shape[0]):
        if i == 0:
            old = next(c)
        else:
            old = current

        current = next(c)
        yield old, current


ti.init(
    arch=ti.cpu,
    cfg_optimization=False,
    opt_level=1,
    fast_math=False,
    advanced_optimization=False,
)

NMAXV = 16  # Maximum vertices per polygon
ti.f32 = ti.f32
PC2TYPE = ti.types.matrix(n=NMAXV, m=2, dtype=ti.f32)
PC3TYPE = ti.types.matrix(n=NMAXV, m=3, dtype=ti.f32)
P2STRUCT = ti.types.struct(polygon=PC2TYPE, k=ti.i32)
P3STRUCT = ti.types.struct(polygon=PC3TYPE, k=ti.i32)
POINT2TYPE = ti.types.vector(n=2, dtype=ti.f32)
POINT3TYPE = ti.types.vector(n=3, dtype=ti.f32)

FINFOTYPE = ti.types.struct(
    vi=P3STRUCT,
    fn=POINT3TYPE,
    fc=POINT3TYPE,
    a=ti.f32,
    vis=ti.u1,
    d=ti.f32,
    vip=P2STRUCT,
)
FINFOFIELD = None
SMTYPE = None
rv = ti.types.vector(n=3, dtype=ti.f32)([0.2, 1.0, 0.2]).normalized()


def _poly_area_r3(verts: np.ndarray) -> float:
    a = 0.0
    if verts.shape[0] > 2:
        for i in range(verts.shape[0] - 2):
            e1 = verts[i + 1, :] - verts[0, :]
            e2 = verts[i + 2, :] - verts[0, :]
            a += 0.5 * np.linalg.norm(np.cross(e1, e2))
    return a


def load_finfo(obj_path) -> None:
    global FINFOFIELD, SMTYPE

    obj = pv.get_reader(obj_path).read().clean()
    f = []
    i = 0

    while True:
        f.append(obj.faces[i + 1 : i + 1 + obj.faces[i]])
        i += obj.faces[i] + 1
        if i == obj.faces.size:
            break
        if i > obj.faces.size:
            raise RuntimeError()

    FINFOFIELD = FINFOTYPE.field(shape=len(f), layout=ti.Layout.AOS)
    SMTYPE = ti.types.matrix(len(f), len(f), dtype=ti.u1)

    for i, fi in enumerate(f):
        vi = np.array(obj.points[fi]).astype(np.float32)
        fn = np.cross(vi[1, :] - vi[0, :], vi[2, :] - vi[0, :])
        fn /= np.linalg.norm(fn)
        fc = np.mean(vi, axis=0)
        num_verts = vi.shape[0]
        poly = PC3TYPE(0.0)
        poly[:num_verts, :] = vi
        FINFOFIELD[i].vi = P3STRUCT(polygon=poly, k=num_verts)
        FINFOFIELD[i].fn = POINT3TYPE(*fn.astype(np.float32))
        FINFOFIELD[i].fc = POINT3TYPE(*fc.astype(np.float32))
        FINFOFIELD[i].a = _poly_area_r3(vi)

    return SMTYPE, FINFOFIELD


def gen_cache(naz: int, nel: int) -> ti.field:
    cache = SMTYPE.field(shape=(naz, nel))

    @ti.kernel
    def gen_cache() -> int:
        ti.loop_config(serialize=True)
        for i, j in ti.ndrange(naz, nel):
            az = i / naz * ti.math.pi * 2
            el = j / (nel - 1) * ti.math.pi - ti.math.pi / 2
            v = sph_to_cart(az, el)
            sm = compute_overlaps(v)
            cache[i, j] = sm
        return 0

    gen_cache()
    return cache


@ti.func
def sph_to_cart(az: ti.f32, el: ti.f32) -> ti.math.vec3:
    cos_theta = ti.cos(el)
    x = cos_theta * ti.cos(az)
    y = cos_theta * ti.sin(az)
    z = ti.sin(el)
    return ti.math.vec3(x, y, z)


@ti.func
def poly_on_poly_ti(t1: P3STRUCT, t3: P3STRUCT, v: ti.math.vec3) -> P2STRUCT:
    t3n = ti.math.cross(
        t3.polygon[1, :] - t3.polygon[0, :], t3.polygon[2, :] - t3.polygon[0, :]
    ).normalized()
    t1p = P3STRUCT()
    t1p.k = t1.k
    for i in range(t1.k):
        t1p.polygon[i, :] = proj_to_plane_along_dir(
            t1.polygon[i, :], v, t3.polygon[0, :], t3n
        )

    e1 = (t3.polygon[1, :] - t3.polygon[0, :]).normalized()
    e2 = ti.math.cross(t3n, e1)
    m = ti.Matrix.rows([e1, e2, t3n])
    t1p2_poly = t1p.polygon @ m.transpose()
    t3p2_poly = t3.polygon @ m.transpose()

    t1p2 = P2STRUCT(polygon=t1p2_poly[:, :2], k=t1.k)
    t3p2 = P2STRUCT(polygon=t3p2_poly[:, :2], k=t3.k)
    clip = clip_ti(t1p2, t3p2)
    return clip


@ti.func
def proj_to_plane_along_dir(
    v0: ti.math.vec3, vd: ti.math.vec3, pv: ti.math.vec3, pn: ti.math.vec3
) -> ti.math.vec3:
    pd = ti.math.dot(pv, pn)
    d2p = ti.math.dot(v0, pn) - pd
    dfac = ti.math.dot(vd, pn)
    return v0 - vd * (d2p / dfac)


@ti.func
def compute_overlaps(v: ti.math.vec3):
    e1 = ti.math.cross(v, rv).normalized()
    e2 = ti.math.cross(v, e1)

    ti.loop_config(serialize=True)
    for i in range(FINFOFIELD.shape[0]):
        FINFOFIELD[i].vip.polygon = ti.zero(FINFOFIELD[i].vip.polygon)
        fi = FINFOFIELD[i]
        FINFOFIELD[i].vis = ti.math.dot(fi.fn, v) > 0
        FINFOFIELD[i].d = ti.math.dot(v - fi.fc, v)
        ti.loop_config(serialize=True)
        for j in range(NMAXV):
            if j == fi.vi.k:
                FINFOFIELD[i].vip.k = fi.vi.k
                break
            pp = fi.vi.polygon[j, :]
            vi_plane = pp - ti.math.dot(pp, v) * v
            vip1 = ti.math.dot(vi_plane, e1)
            vip2 = ti.math.dot(vi_plane, e2)
            FINFOFIELD[i].vip.polygon[j, :] = ti.math.vec2(vip1, vip2)

    sm = SMTYPE(False)
    ti.loop_config(serialize=True)
    for i, j in ti.ndrange(FINFOFIELD.shape[0], FINFOFIELD.shape[0]):
        fi, fj = FINFOFIELD[i], FINFOFIELD[j]
        if i != j and fi.vis and fj.vis and fi.d < fj.d:
            clp_area = intersection_area_ti(fj.vip, fi.vip)
            if clp_area > 1e-7:
                sm[i, j] = True
    return sm


@ti.func
def all_areas_ti(p1: P2STRUCT, p2: P2STRUCT) -> tuple:
    a1 = poly_area_ti(p1)
    a2 = poly_area_ti(p2)
    ai = intersection_area_ti(p1, p2)
    au = a1 + a2 - ai  # area of the union between 1 and 2
    a1n2 = a1 - ai  # area of 1 not including 2
    a2n1 = a2 - ai  # area of 2 not including 1
    axor = au - ai  # area of 1 and 2 not including the intersection
    return a1, a2, ai, au, a1n2, a2n1, axor


@ti.func
def tri_area(v1: ti.math.vec2, v2: ti.math.vec2, v3: ti.math.vec2) -> float:
    return 0.5 * ti.abs(
        v1[0] * (v2[1] - v3[1]) + v2[0] * (v3[1] - v1[1]) + v3[0] * (v1[1] - v2[1])
    )


@ti.func
def poly_area_ti(p: P2STRUCT) -> ti.f32:
    a = 0.0
    if p.k > 2:
        ti.loop_config(serialize=True)
        for i in range(p.k - 2):
            a += tri_area(p.polygon[0, :], p.polygon[i + 1, :], p.polygon[i + 2, :])
    return a


@ti.func
def intersection_area_ti(p1: P2STRUCT, p2: P2STRUCT) -> ti.f32:
    clp = clip_ti(p1, p2)
    return poly_area_ti(clp)


@ti.func
def is_tri_ccw(v1: ti.math.vec2, v2: ti.math.vec2, v3: ti.math.vec2) -> bool:
    return (
        v1[0] * (v2[1] - v3[1]) + v2[0] * (v3[1] - v1[1]) + v3[0] * (v1[1] - v2[1])
    ) > 0


@ti.func
def is_inside(p1: ti.math.vec2, p2: ti.math.vec2, q: ti.math.vec2) -> ti.u1:
    R = (p2[0] - p1[0]) * (q[1] - p1[1]) - (p2[1] - p1[1]) * (q[0] - p1[0])
    return R <= -1e-4


@ti.func
def compute_intersection(
    p1: ti.math.vec2, p2: ti.math.vec2, p3: ti.math.vec2, p4: ti.math.vec2
) -> ti.math.vec2:
    v = POINT2TYPE(0.0)
    # if first line is vertical
    if p2[0] - p1[0] == 0:
        # slope and intercept of second line
        m2 = (p4[1] - p3[1]) / (p4[0] - p3[0])
        b2 = p3[1] - m2 * p3[0]

        v.x = p1[0]
        # y-coordinate of intersection
        v.y = m2 * v.x + b2

    # if second line is vertical
    elif p4[0] - p3[0] == 0:
        # slope and intercept of first line
        m1 = (p2[1] - p1[1]) / (p2[0] - p1[0])
        b1 = p1[1] - m1 * p1[0]

        v.x = p3[0]
        # y-coordinate of intersection
        v.y = m1 * v.x + b1

    # if neither line is vertical
    else:
        m1 = (p2[1] - p1[1]) / (p2[0] - p1[0])
        b1 = p1[1] - m1 * p1[0]

        # slope and intercept of second line
        m2 = (p4[1] - p3[1]) / (p4[0] - p3[0])
        b2 = p3[1] - m2 * p3[0]

        # x-coordinate of intersection
        v.x = (b2 - b1) / (m1 - m2)

        # y-coordinate of intersection
        v.y = m1 * v.x + b1

    return v


@ti.kernel
def clip_many_ti(sp: P2STRUCT, cp: P2STRUCT) -> P2STRUCT:
    res = P2STRUCT()
    n = int(1e6)
    for _i in range(n):
        res = clip_ti(sp, cp)
    return res


@ti.kernel
def clip_one(sp: P2STRUCT, cp: P2STRUCT, side: int) -> P2STRUCT:
    return clip_ti(sp, cp, side)


@ti.func
def clip_ti(sp: ti.template(), cp: ti.template(), side: int) -> ti.template():
    k = sp.k
    n_clip_edges = cp.k

    subject_polygon = PC2TYPE(0.0)
    for i in range(k):
        subject_polygon[i, :] = sp.polygon[i, :].cast(ti.f32)

    cp_ccw = is_tri_ccw(cp.polygon[0, :], cp.polygon[1, :], cp.polygon[2, :])
    clipping_polygon = PC2TYPE(0.0)
    for i in range(n_clip_edges):
        if not cp_ccw:
            clipping_polygon[i, :] = cp.polygon[i, :].cast(ti.f32)
        else:
            clipping_polygon[n_clip_edges - i - 1, :] = cp.polygon[i, :].cast(ti.f32)

    final_polygon = PC2TYPE(0.0)
    next_polygon = subject_polygon

    i = side

    oldk = k
    k = 0

    pi = i - 1
    if i == 0:
        pi = n_clip_edges - 1

    c_edge_start = clipping_polygon[pi, :]
    c_edge_end = clipping_polygon[i, :]

    ti.loop_config(serialize=True)
    for j in range(oldk):
        pj = j - 1
        if j == 0:
            pj = oldk - 1

        s_edge_start = next_polygon[pj, :]
        s_edge_end = next_polygon[j, :]

        if is_inside(c_edge_start, c_edge_end, s_edge_end):
            if not is_inside(c_edge_start, c_edge_end, s_edge_start):
                final_polygon[k, :] = compute_intersection(
                    s_edge_start, s_edge_end, c_edge_start, c_edge_end
                )
                k += 1
            final_polygon[k, :] = s_edge_end
            k += 1
        elif is_inside(c_edge_start, c_edge_end, s_edge_start):
            final_polygon[k, :] = compute_intersection(
                s_edge_start, s_edge_end, c_edge_start, c_edge_end
            )
            k += 1
    return P2STRUCT(polygon=final_polygon, k=k)


if __name__ == '__main__':
    subject_polygon = ti.Matrix(
        np.array(
            [
                (0, 3),
                (0.5, 0.5),
                (3, 0),
                (0.5, -0.5),
                (0, -3),
                (-0.5, -0.5),
                (-3, 0),
                (-0.5, 0.5),
            ]
        )
    )
    clipping_polygon = ti.Matrix(np.array([(-2, -2), (-2, 2), (2, 2), (2, -2)]))

    spfull = PC2TYPE(0.0)
    spfull[: subject_polygon.n, :] = subject_polygon
    sp = P2STRUCT(polygon=spfull, k=subject_polygon.n)

    cpfull = PC2TYPE(0.0)
    cpfull[: clipping_polygon.n, :] = clipping_polygon
    cp = P2STRUCT(polygon=cpfull, k=clipping_polygon.n)

    plt.figure(figsize=(9, 6))
    for i in range(4):
        plt.subplot(2, 2, i + 1)
        sp = clip_one(sp, cp, i)
        clipped_polygon = sp['polygon'][: sp['k'], :]

        plot_poly(subject_polygon, c='m', linewidth=4, label='Subject polygon')
        plot_poly(clipping_polygon, c='k', linewidth=4, label='Clipping polygon')
        plt.plot(
            *np.array((clipping_polygon[i, :], clipping_polygon[(i - 1) % 4, :])).T,
            'c--',
            linewidth=2,
            label='Clipping edge',
        )

        plot_poly(
            clipped_polygon,
            c='lime',
            marker='.',
            linewidth=1.6,
            label='Clipped polygon',
        )
        plt.grid()
        plt.xlabel('$x$ distance units')
        plt.ylabel('$y$ distance units')
        plt.title(f'Step {i+1}/4')
        plt.ylim(-3.5, 3.75)

    plt.gcf().suptitle('Sutherland-Hodgeman Polygon Clipping')
    plt.subplot(2, 2, 2)
    plt.legend(bbox_to_anchor=(1.05, 1.02))
    plt.tight_layout()
    plt.show()