Light Curve Ambiguities

Demonstrating various ways a light curve can be ambiguous as a function of the object and its attitude profile.

import matplotlib.pyplot as plt
import numpy as np

import mirage as mr
import mirage.vis as mrv

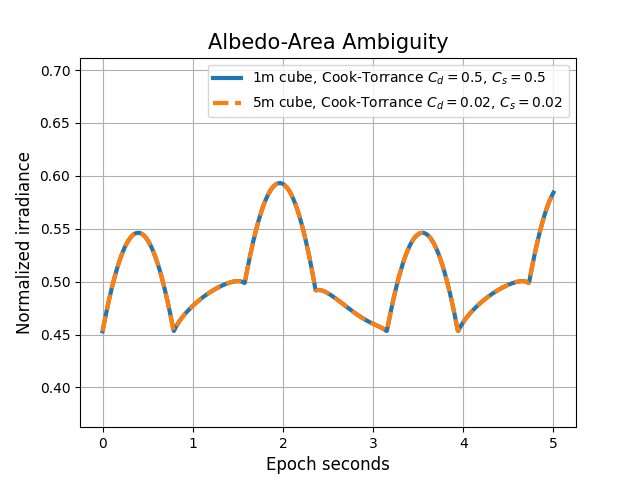
Albedo-area ambiguity

brdf = mr.Brdf('cook-torrance', cd=0.5, cs=0.5, n=5.0)
dates, epsecs = mr.date_linspace(
    mr.now(), mr.now() + mr.seconds(5), 1000, return_epsecs=True
)
attitude = mr.RbtfAttitude(
    w0=1.0 * mr.hat(np.array([[0.1, 0.0, 1.0]])),
    q0=mr.hat(np.array([0.0, 0.0, 0.0, 1.0])),
    itensor=np.diag([1.0, 2.0, 3.0]),
)
q_of_t, _ = attitude.propagate(epsecs)
svi = np.array([[1.0, 0.0, 0.0]])
ovi = np.array([1.0, 1.0, 0.0])

svb = mr.stack_mat_mult_vec(mr.quat_to_dcm(q_of_t), svi)
ovb = mr.stack_mat_mult_vec(mr.quat_to_dcm(q_of_t), ovi)

sf = 5.0
obj1 = mr.SpaceObject('cube.obj')
obj2 = mr.SpaceObject('cube.obj')
obj2.v *= sf
obj2.build_properties()

lc1 = obj1.convex_light_curve(brdf, svb, ovb)
plt.plot(
    epsecs, lc1, lw=3, label=f'1m cube, Cook-Torrance $C_d={brdf.cd}$, $C_s={brdf.cs}$'
)
brdf.cd /= sf**2
brdf.cs /= sf**2
lc2 = obj2.convex_light_curve(brdf, svb, ovb)

plt.plot(
    epsecs,
    lc2,
    '--',
    lw=3,
    label=f'{sf:.0f}m cube, Cook-Torrance $C_d={brdf.cd}$, $C_s={brdf.cs}$',
)
mrv.texit('Albedo-Area Ambiguity', 'Epoch seconds', 'Normalized irradiance')
plt.legend()
plt.ylim([np.min(lc1) * 0.8, np.max(lc1) * 1.2])
plt.show()

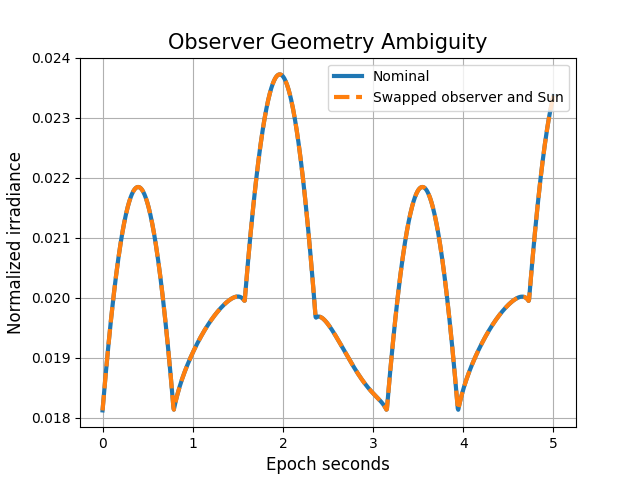
Observation geometry ambiguity We know that the light curve is symmetric when the positions of the observer and sun are swapped.

lc1 = obj1.convex_light_curve(brdf, svb, ovb)
plt.plot(epsecs, lc1, lw=3, label='Nominal')
lc2 = obj1.convex_light_curve(brdf, ovb, svb)
plt.plot(epsecs, lc2, '--', lw=3, label='Swapped observer and Sun')
mrv.texit('Observer Geometry Ambiguity', 'Epoch seconds', 'Normalized irradiance')
plt.legend()
plt.show()

Non-convex observability

# obj1 = mr.SpaceObject("cylinder.obj")
# obj2 = mr.SpaceObject("collapsed_cyl.obj")

# lc1 = obj1.convex_light_curve(brdf, svb, ovb)
# plt.plot(epsecs, lc1, lw=3, label=f"Convex")
# lc2 = obj2.convex_light_curve(brdf, svb, ovb)
# plt.plot(epsecs, lc2, '--', lw=3, label=f"Non-convex")
# mrv.texit('Non-convex Ambiguity', 'Epoch seconds', 'Normalized irradiance')
# plt.legend()
# plt.show()