Note

Go to the end to download the full example code.

Types of Light Curves#

Plotting light curves for a variety of object types and attitude profiles

# isort: off

import datetime
from typing import Any

import matplotlib.pyplot as plt
import numpy as np
import pyvista as pv
from matplotlib.animation import FuncAnimation
import mirage as mr
import mirage.vis as mrv
from PIL import Image

Case 1: The light curve of a cube

integration_time_s = 1.0  # seconds
obj = mr.SpaceObject('cube.obj', identifier='GOES 15')

pl = pv.Plotter()
mrv.render_spaceobject(pl, obj)
mrv.plot_basis(
    pl,
    np.eye(3),
    labels=['$\hat{x}$', '$\hat{y}$', '$\hat{z}$'],
    scale=np.max(mr.vecnorm(obj.v)),
    shape_opacity=0.5,
)
pl.show_bounds()
pl.show()
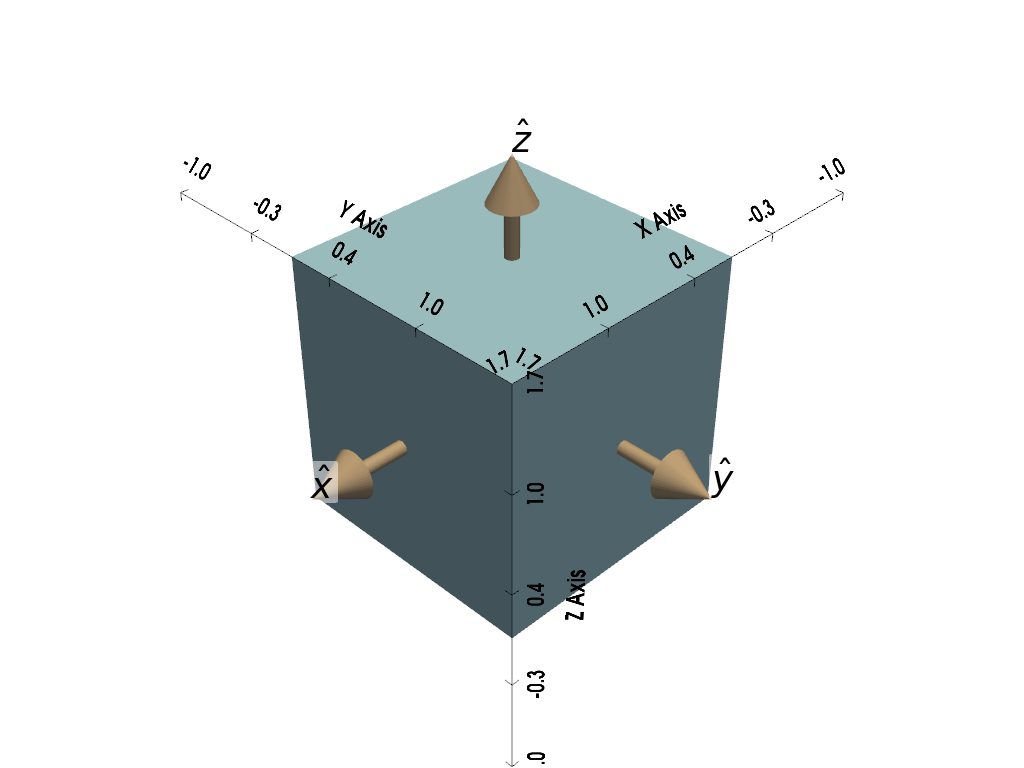
light curves types

Setup

station = mr.Station(preset='pogs')
brdf = mr.Brdf(name='phong', cd=0.7, cs=0.3, n=5)
attitude = mr.RbtfAttitude(
    w0=0.1 * mr.hat(np.array([[1.0, 2.0, 1.0]])),
    q0=np.array([0.0, 0.0, 0.0, 1.0]),
    itensor=np.diag([1.0, 2.0, 3.0]),
)
idate = mr.utc(2023, 3, 26, 5)
dates, epsecs = mr.date_arange(
    idate, idate + mr.minutes(1), mr.seconds(1), return_epsecs=True
)

print(attitude.w0)
print(idate)

[0.04082483 0.08164966 0.04082483]
2023-03-26 05:00:00+00:00

Determining inertial positions of the Sun, observer, and object

r_obj_j2k = obj.propagate(dates)
sv = mr.sun(dates)
ov = station.j2000_at_dates(dates)
svi = sv - r_obj_j2k
ovi = ov - r_obj_j2k

Plotting the spin and orientation over time

q_of_t, w_of_t = attitude.propagate(epsecs)
dcms_of_t = mr.quat_to_dcm(q_of_t)
svb = mr.stack_mat_mult_vec(dcms_of_t, svi)
ovb = mr.stack_mat_mult_vec(dcms_of_t, ovi)

plt.figure(figsize=(12, 3))
plt.subplot(1, 4, 1)
plt.plot(epsecs, q_of_t)
mrv.texit('$q(t)$', 'Seconds after epoch', '', ['$q_1$', '$q_2$', '$q_3$', '$q_4$'])
plt.subplot(1, 4, 2)
plt.plot(epsecs, w_of_t)
mrv.texit(
    '$\omega(t)$',
    'Seconds after epoch',
    r'$\left[ \frac{rad}{s} \right]$',
    ['$\omega_1$', '$\omega_2$', '$\omega_3$'],
)
plt.subplot(1, 4, 3)
plt.plot(epsecs, svb)
mrv.texit(
    '${}^{\mathcal{B}}\mathbf{r}_{\mathrm{Sun}}(t) - {}^{\mathcal{B}}\mathbf{r}_{\mathrm{obj}}(t)$',
    'Seconds after epoch',
    '[km]',
    ['$x$', '$y$', '$z$'],
)
plt.subplot(1, 4, 4)
plt.plot(epsecs, ovb)
mrv.texit(
    '${}^{\mathcal{B}}\mathbf{r}_{\mathrm{obs}}(t) - {}^{\mathcal{B}}\mathbf{r}_{\mathrm{obj}}(t)$',
    'Seconds after epoch',
    '[km]',
    ['$x$', '$y$', '$z$'],
)
plt.tight_layout()
# plt.show()

svb = mr.hat(svb)
ovb = mr.hat(ovb)
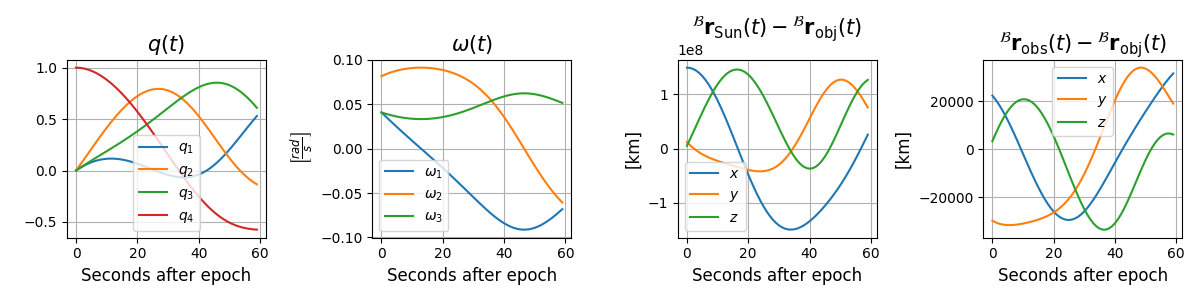
$q(t)$, $\omega(t)$, ${}^{\mathcal{B}}\mathbf{r}_{\mathrm{Sun}}(t) - {}^{\mathcal{B}}\mathbf{r}_{\mathrm{obj}}(t)$, ${}^{\mathcal{B}}\mathbf{r}_{\mathrm{obs}}(t) - {}^{\mathcal{B}}\mathbf{r}_{\mathrm{obj}}(t)$

Plotting the reflection matrix

G = brdf.compute_reflection_matrix(svb, ovb, obj.unique_normals)
lc = G @ obj.unique_areas

plt.imshow(G, cmap='plasma', aspect='auto', interpolation='none')
mrv.texit('Reflection Matrix $G$', 'Normal index $i$', 'Time index $j$', grid=False)
# plt.show()
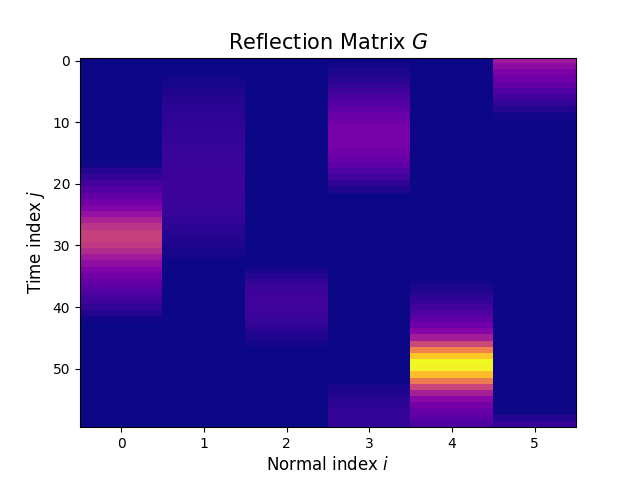
Reflection Matrix $G$

Plotting the light curve

plt.plot(epsecs, lc)
mrv.texit('Normalized Light Curve $\hat{I}(t)$', 'Seconds after epoch', '[nondim]')
# plt.show()
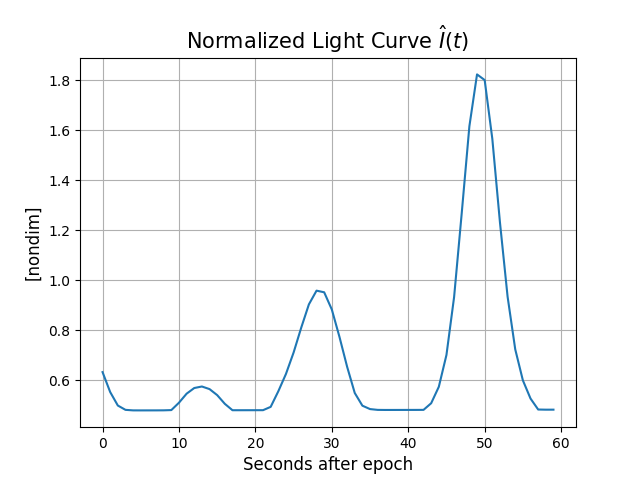
Normalized Light Curve $\hat{I}(t)$

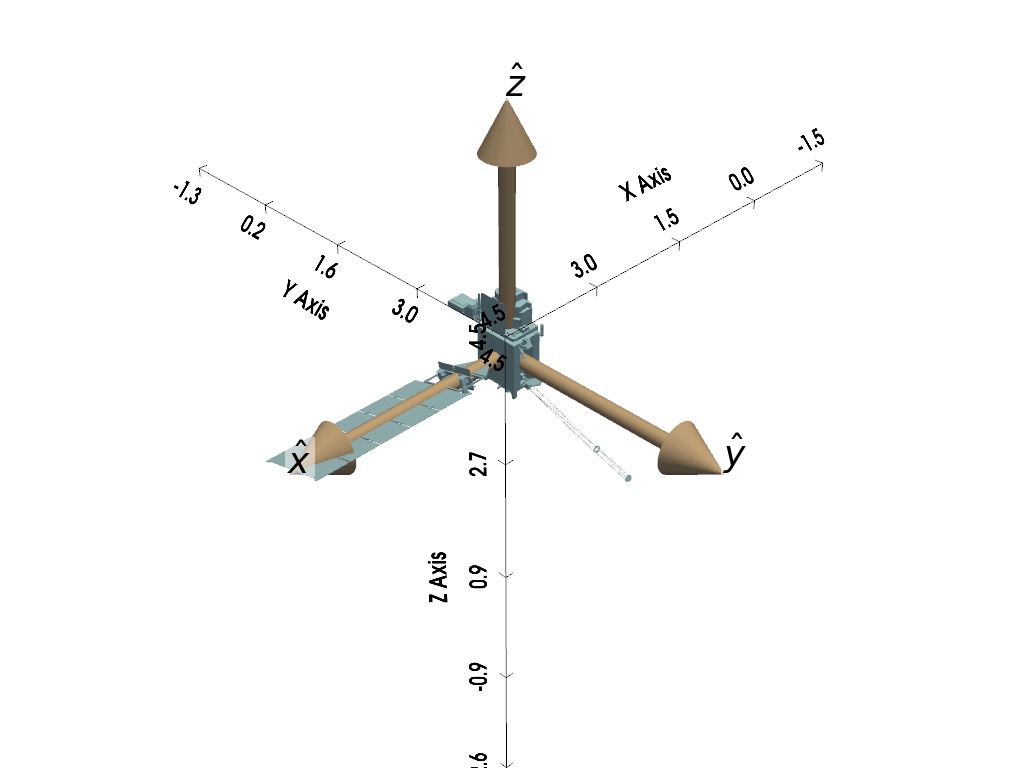
Case 2: a box-wing

obj = mr.SpaceObject('matlib_goes17.obj', identifier=26360)
msf = 0.1

pl = pv.Plotter()
mrv.render_spaceobject(pl, obj)
mrv.plot_basis(
    pl,
    np.eye(3),
    labels=['$\hat{x}$', '$\hat{y}$', '$\hat{z}$'],
    scale=np.max(mr.vecnorm(obj.v)),
    shape_opacity=0.5,
)
pl.show_bounds()
# pl.show()
light curves types
<CubeAxesActor(0x139d09a00) at 0x3272e7460>

Setup

station = mr.Station(preset='pogs')
station.constraints = [
    mr.SnrConstraint(3),
    mr.ElevationConstraint(15),
    mr.TargetIlluminatedConstraint(),
    mr.ObserverEclipseConstraint(station),
    mr.MoonExclusionConstraint(30),
]
brdf = mr.Brdf(name='phong')
attitude = mr.RbtfAttitude(
    w0=0.01 * mr.hat(np.array([[1.0, 0.0, 1.0]])),
    q0=np.array([0.0, 0.0, 0.0, 1.0]),
    itensor=np.diag([1.0, 2.0, 2.0]),
)
idate = mr.utc(2022, 12, 9, 8)
dates, epsecs = mr.date_arange(
    idate, idate + mr.minutes(30), mr.seconds(10), return_epsecs=True
)

print(idate)
print(attitude.w0)

2022-12-09 08:00:00+00:00
[0.00707107 0.         0.00707107]

Determining inertial positions of the Sun, observer, and object

r_obj_j2k = obj.propagate(dates)
sv = mr.sun(dates)
ov = station.j2000_at_dates(dates)
svi = sv - r_obj_j2k
ovi = ov - r_obj_j2k

# pl = pv.Plotter()
# mrv.render_observation_scenario(pl, dates, station, mr.hat(-ovi), sensor_extent_km=36e3, night_lights=True)
# pl.show()

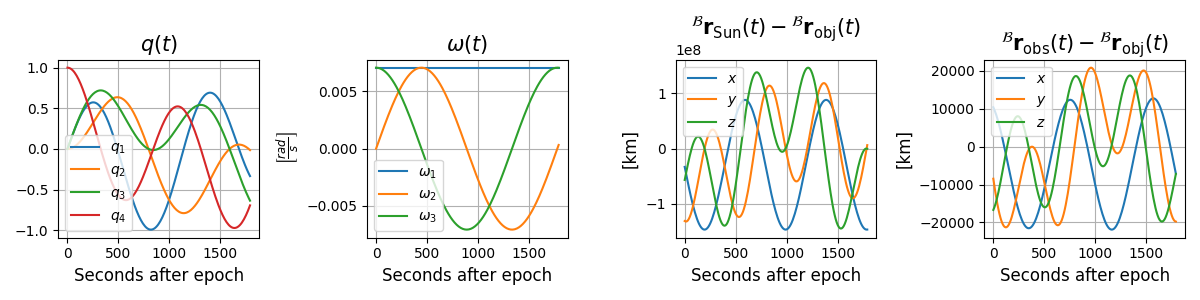
Plotting the spin and orientation over time

q_of_t, w_of_t = attitude.propagate(epsecs)
dcms_of_t = mr.quat_to_dcm(q_of_t)
svb = mr.stack_mat_mult_vec(dcms_of_t, svi)
ovb = mr.stack_mat_mult_vec(dcms_of_t, ovi)

plt.figure(figsize=(12, 3))
plt.subplot(1, 4, 1)
plt.plot(epsecs, q_of_t)
mrv.texit('$q(t)$', 'Seconds after epoch', '', ['$q_1$', '$q_2$', '$q_3$', '$q_4$'])
plt.subplot(1, 4, 2)
plt.plot(epsecs, w_of_t)
mrv.texit(
    '$\omega(t)$',
    'Seconds after epoch',
    r'$\left[ \frac{rad}{s} \right]$',
    ['$\omega_1$', '$\omega_2$', '$\omega_3$'],
)
plt.subplot(1, 4, 3)
plt.plot(epsecs, svb)
mrv.texit(
    '${}^{\mathcal{B}}\mathbf{r}_{\mathrm{Sun}}(t) - {}^{\mathcal{B}}\mathbf{r}_{\mathrm{obj}}(t)$',
    'Seconds after epoch',
    '[km]',
    ['$x$', '$y$', '$z$'],
)
plt.subplot(1, 4, 4)
plt.plot(epsecs, ovb)
mrv.texit(
    '${}^{\mathcal{B}}\mathbf{r}_{\mathrm{obs}}(t) - {}^{\mathcal{B}}\mathbf{r}_{\mathrm{obj}}(t)$',
    'Seconds after epoch',
    '[km]',
    ['$x$', '$y$', '$z$'],
)
plt.tight_layout()
plt.show()
$q(t)$, $\omega(t)$, ${}^{\mathcal{B}}\mathbf{r}_{\mathrm{Sun}}(t) - {}^{\mathcal{B}}\mathbf{r}_{\mathrm{obj}}(t)$, ${}^{\mathcal{B}}\mathbf{r}_{\mathrm{obs}}(t) - {}^{\mathcal{B}}\mathbf{r}_{\mathrm{obj}}(t)$

Plotting the light curve

lc, aux_data = station.observe_light_curve(
    obj,
    attitude,
    brdf,
    dates,
    integration_time_s=integration_time_s,
    use_engine=True,
    model_scale_factor=msf,
    save_imgs=True,
    instances=1,
)


imgs = []
for i in range(len(dates)):
    imgs.append(2 * np.array(Image.open(f'out/frame{i + 1}.png'))[:, :, 0])

save a gif animation of the images in the out/ directory

fig = plt.figure(figsize=(10, 4))
plt.subplot(1, 2, 1)
im = plt.imshow(imgs[0], cmap='gray')
mrv.texit('Rendered Scene', '', '')
plt.xticks([])
plt.yticks([])
plt.subplot(1, 2, 2)
lci = lc().filled(np.nan)
plt.plot(epsecs, lci)
plt.yscale('log')

pt = plt.scatter(epsecs[0], lci[0], color='r')
plt.gca().set_aspect('auto')
mrv.texit('Light Curve $I(t)$', 'Seconds after epoch', '[ADU]')


def animate(i):
    im.set_data(imgs[i])
    pt.set_offsets((epsecs[i], lci[i]))
    return im, pt


frames = len(dates)
anim_time = 10
fps = frames / anim_time
interval = 1000 / fps
anim = FuncAnimation(fig, animate, frames=frames, interval=interval, blit=True)
anim.save('out/animation.gif')


lcs = np.array([lc() for i in range(1000)])
mean_lcs = np.mean(lcs, axis=0)
var_lcs = np.var(lcs, axis=0)

for stdev in [1, 2, 3]:
    plt.fill_between(
        epsecs,
        mean_lcs - (stdev - 1) * np.sqrt(var_lcs),
        mean_lcs - stdev * np.sqrt(var_lcs),
        alpha=0.4 - 0.1 * stdev,
        color='b',
        edgecolor=None,
        label=f'{stdev}$\sigma$',
    )
    plt.fill_between(
        epsecs,
        mean_lcs + (stdev - 1) * np.sqrt(var_lcs),
        mean_lcs + stdev * np.sqrt(var_lcs),
        alpha=0.4 - 0.1 * stdev,
        color='b',
        edgecolor=None,
    )

plt.plot(epsecs, mean_lcs, lw=1, color='k', label='Mean')
plt.yscale('log')
mrv.texit('Light Curve $I(t)$', 'Seconds after epoch', '[ADU]')
plt.legend()
plt.show()

Without uncertainty

plt.figure()
lc, aux_data = station.observe_light_curve(
    obj,
    attitude,
    brdf,
    dates,
    integration_time_s=integration_time_s,
    use_engine=True,
    model_scale_factor=msf,
)

lcs = np.array([lc() for i in range(1000)])
mean_lcs = np.mean(lcs, axis=0)

plt.plot(epsecs, mean_lcs, lw=1, color='k')
plt.yscale('log')
mrv.texit('Noiseless Light Curve $I(t)$', 'Seconds after epoch', '[ADU]')
plt.legend()
plt.show()
Noiseless Light Curve $I(t)$
/Users/liamrobinson/Documents/maintained-research/mirage/examples/01-light_curves/light_curves_types.py:312: UserWarning: No artists with labels found to put in legend.  Note that artists whose label start with an underscore are ignored when legend() is called with no argument.
  plt.legend()

Defining the object and attitude combos

def aligned_nadir_constrained_sun_attitude(
    obj: mr.SpaceObject, dates: np.ndarray[datetime.datetime, Any]
) -> mr.AlignedAndConstrainedAttitude:
    r_obj_j2k = obj.propagate(dates)
    sv = mr.sun(dates)
    nadir = -mr.hat(r_obj_j2k)
    return mr.AlignedAndConstrainedAttitude(
        v_align=nadir, v_const=sv, dates=dates, axis_order=(1, 2, 0)
    )


station = mr.Station(preset='pogs')
station.constraints = [
    mr.SnrConstraint(3),
    mr.ElevationConstraint(10),
    mr.TargetIlluminatedConstraint(),
    mr.ObserverEclipseConstraint(station),
    mr.VisualMagnitudeConstraint(18),
    mr.MoonExclusionConstraint(10),
]

inertially_fixed_attitude = mr.SpinStabilizedAttitude(
    0.0, np.array([1.0, 0.0, 0.0]), 2e5, 0.0
)
tumbling_attitude = mr.RbtfAttitude(
    1e-2 * np.array([1.0, 0.0, 1.0]),
    np.array([0.0, 0.0, 0.0, 1.0]),
    np.diag([1.0, 2.0, 2.0]),
)
brdf_specular = mr.Brdf(cd=0.2, cs=0.4, n=10, name='phong')
brdf_phong = mr.Brdf(name='phong')

combos = [
    dict(
        name='Lincoln Calibration Sphere 1',
        obj=mr.SpaceObject('sphere_uv.obj', identifier='LCS 1'),
        attitude=inertially_fixed_attitude,
        brdf=brdf_specular,
        size=1.16 / 2,
    ),
    dict(
        name='Delta II Rocket Body',
        obj=mr.SpaceObject('matlib_saturn_v_sii.obj', identifier=34382),
        attitude=tumbling_attitude,
        brdf=brdf_phong,
        size=None,
    ),
]

idate = mr.utc(2023, 3, 26, 5)
dates = mr.date_arange(idate, idate + mr.days(1), mr.seconds(10))

for combo in combos:
    if combo['size'] is not None:
        vmax = np.max(mr.vecnorm(combo['obj'].v))
        combo['obj'].v /= vmax / combo['size']
        delattr(combo['obj'], 'file_name')
    lc_sampler, _ = station.observe_light_curve(
        obj=combo['obj'],
        obj_attitude=combo['attitude'],
        brdf=combo['brdf'],
        dates=dates,
        integration_time_s=integration_time_s,
        use_engine=True,
    )
    lc = lc_sampler()

    plt.figure(figsize=(10, 5))
    plt.scatter(dates, lc, s=1)
    mrv.texit(combo['name'], 'Date', 'ADU')
    plt.show()
  • Lincoln Calibration Sphere 1
  • Delta II Rocket Body
Model file sphere_uv.obj not found in current model folder ('/Users/liamrobinson/Documents/maintained-research/mirage/mirage/resources/models'), checking model repository...
Attempting to download sphere_uv.obj and its associated material file from the model repository...
Requesting: https://raw.githubusercontent.com/ljrobins/mirage-models/main//accurate_sats/sphere_uv.obj
Model files were downloaded successfully!
Model file matlib_saturn_v_sii.obj not found in current model folder ('/Users/liamrobinson/Documents/maintained-research/mirage/mirage/resources/models'), checking model repository...
Attempting to download matlib_saturn_v_sii.obj and its associated material file from the model repository...
Requesting: https://raw.githubusercontent.com/ljrobins/mirage-models/main//accurate_sats/matlib_saturn_v_sii.obj
Model files were downloaded successfully!

Total running time of the script: (1 minutes 9.163 seconds)

Gallery generated by Sphinx-Gallery