Euler Angle Sequence

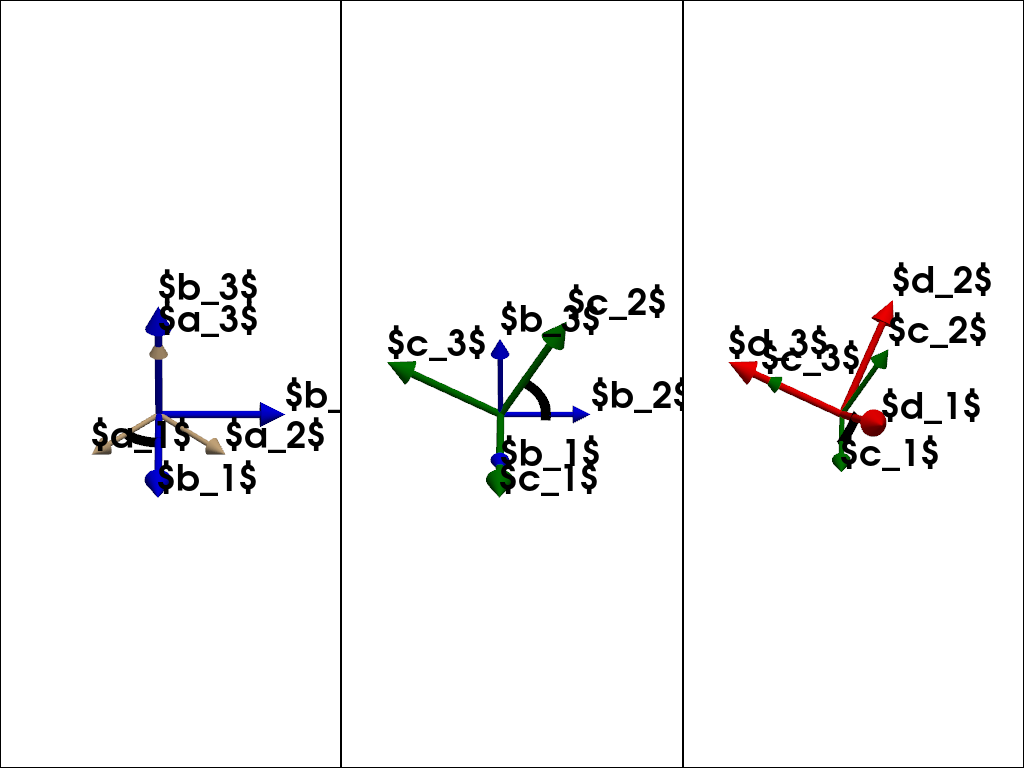
Three consecutive axis rotations forming an Euler angle sequence

import numpy as np
import pyvista as pv

import mirage as mr
import mirage.vis as mrv

Let’s get the body axis rotation matrices and define an Euler (3-1-3) sequence

r1, r2, r3 = mr.r3(np.pi / 4), mr.r1(np.pi / 3), mr.r3(np.pi / 5)
a = np.eye(3)
ap = r1
app = r2 @ ap
appp = r3 @ app
sc, d = 1.4, 0.5
pl = pv.Plotter(shape=(1, 3))
pl.subplot(0, 0)
mrv.plot_basis(pl, a.T, labels='a')
mrv.plot_basis(pl, ap.T, labels='b', color='blue', scale=sc)
mrv.plot_angle_between(pl, a[0, :], ap[0, :], center=np.array([0, 0, 0]), dist=d)
pl.subplot(0, 1)
mrv.plot_basis(pl, ap.T, labels='b', color='blue')
mrv.plot_basis(pl, app.T, labels='c', color='green', scale=sc)
mrv.plot_angle_between(pl, ap[1, :], app[1, :], center=np.array([0, 0, 0]), dist=d)
pl.subplot(0, 2)
mrv.plot_basis(pl, app.T, labels='c', color='green')
mrv.plot_basis(pl, appp.T, labels='d', color='red', scale=sc)
mrv.plot_angle_between(pl, app[0, :], appp[0, :], center=np.array([0, 0, 0]), dist=d)

pl.link_views()
pl.view_isometric()
pl.camera.zoom(0.8)
pl.show()