Light Curve Uncertainty

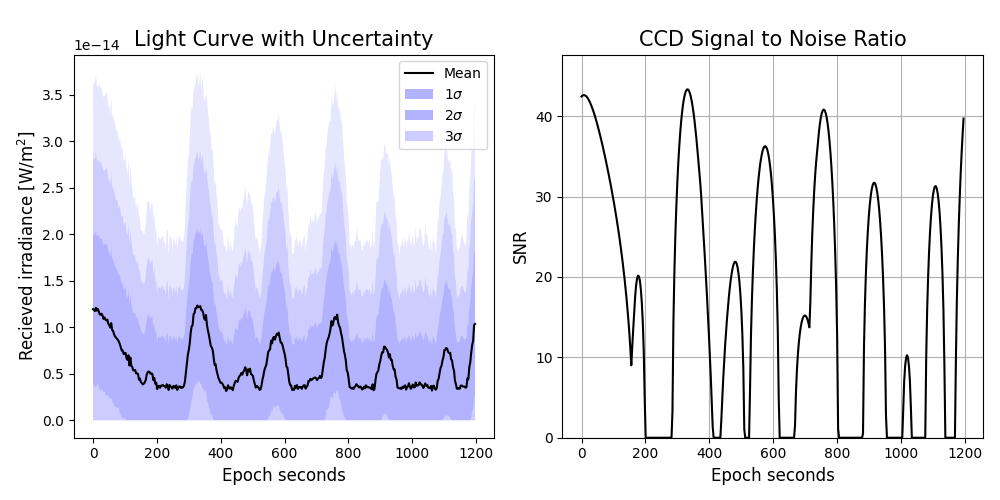
Plotting a realistic light curve with uncertainty

import matplotlib.pyplot as plt
import numpy as np

import mirage as mr
import mirage.vis as mrv

itensor = np.diag([1.0, 2.0, 3.0])
w0 = 1e-2 * mr.hat(np.array([[1.0, 2.0, 1.0]]))
idate = mr.utc(2023, 2, 26, 0)
obs_time = mr.minutes(20)
obs_dt = mr.seconds(3)
integration_time_s = obs_dt.total_seconds()

obj_file = 'cube.obj'

station = mr.Station(preset='pogs')
brdf = mr.Brdf(name='phong', cd=0.5, cs=0.0, n=0)
attitude = mr.RbtfAttitude(w0=w0, q0=np.array([[0.0, 0.0, 0.0, 1.0]]), itensor=itensor)
dates, epsecs = mr.date_arange(idate, idate + obs_time, obs_dt, return_epsecs=True)

rmag = 3e3 * 1e3
diffuse_irrad = (
    mr.AstroConstants.sun_irradiance_vacuum
    * mr.normalized_light_curve_sphere(1.0, 1, np.pi / 2)
    / rmag**2
)
diffuse_mag = mr.irradiance_to_apparent_magnitude(diffuse_irrad)

q_of_t, w_of_t = attitude.propagate(epsecs)
dcms_of_t = mr.quat_to_dcm(q_of_t)

obj = mr.SpaceObject(obj_file, identifier='goes 15')
lc_ccd_signal_sampler, aux_data = station.observe_light_curve(
    obj,
    attitude,
    brdf,
    dates,
    integration_time_s,
    use_engine=False,
    model_scale_factor=0.5,
)

print(np.mean(aux_data['background_mean']))
# endd

plt.figure(figsize=(10, 5))

plt.subplot(1, 2, 1)
lcs_noisy_adu = np.array([lc_ccd_signal_sampler() for _ in range(1000)])
lcs_noisy_irrad = lcs_noisy_adu / (aux_data['sint'] * integration_time_s)
lcs_noisy_mag = lcs_noisy_irrad
var_lcs = np.var(lcs_noisy_mag, axis=0)
mean_lcs = np.mean(lcs_noisy_mag, axis=0)

plt.plot(epsecs, mean_lcs, c='k')
for stdev in [1, 2, 3]:
    plt.fill_between(
        epsecs,
        np.clip(mean_lcs - (stdev - 1) * np.sqrt(var_lcs), 0, np.inf),
        np.clip(mean_lcs - stdev * np.sqrt(var_lcs), 0, np.inf),
        alpha=0.4 - 0.1 * stdev,
        color='b',
        edgecolor=None,
    )
    plt.fill_between(
        epsecs,
        np.clip(mean_lcs + (stdev - 1) * np.sqrt(var_lcs), 0, np.inf),
        np.clip(mean_lcs + stdev * np.sqrt(var_lcs), 0, np.inf),
        alpha=0.4 - 0.1 * stdev,
        color='b',
        edgecolor=None,
    )
mrv.texit(
    'Light Curve with Uncertainty',
    'Epoch seconds',
    'Recieved irradiance [W/m$^2$]',
    grid=False,
    legend=['Mean', '1$\sigma$', '2$\sigma$', '3$\sigma$'],
)

plt.subplot(1, 2, 2)
plt.plot(epsecs, aux_data['snr'], c='k')
plt.ylim(0, np.max(aux_data['snr']) * 1.1)
mrv.texit('CCD Signal to Noise Ratio', 'Epoch seconds', 'SNR')
plt.tight_layout()
plt.show()

/Users/liamrobinson/Documents/maintained-research/mirage/examples/01-light_curves/lc_uncertainty.py:84: SyntaxWarning: invalid escape sequence '\s'
  legend=['Mean', '1$\sigma$', '2$\sigma$', '3$\sigma$'],
/Users/liamrobinson/Documents/maintained-research/mirage/examples/01-light_curves/lc_uncertainty.py:84: SyntaxWarning: invalid escape sequence '\s'
  legend=['Mean', '1$\sigma$', '2$\sigma$', '3$\sigma$'],
/Users/liamrobinson/Documents/maintained-research/mirage/examples/01-light_curves/lc_uncertainty.py:84: SyntaxWarning: invalid escape sequence '\s'
  legend=['Mean', '1$\sigma$', '2$\sigma$', '3$\sigma$'],
WARNING: no observation constraints assigned!
40725.799493609804

Sampling the same light curve on different nights throughout the month

idate = mr.utc(2022, 11, 15, 0)
dates, epsecs = mr.date_arange(idate, idate + obs_time, obs_dt, return_epsecs=True)

for nights in range(4):
    this_dates = dates + mr.days(nights * 60.0)
    lc_ccd_signal_sampler, aux_data = station.observe_light_curve(
        obj,
        attitude,
        brdf,
        this_dates,
        integration_time_s,
        use_engine=False,
        model_scale_factor=0.5,
    )

    print(np.mean(aux_data['background_mean']))

    plt.subplot(2, 2, nights + 1)

    lcs_noisy_adu = np.array([lc_ccd_signal_sampler() for _ in range(1000)])
    lcs_noisy_irrad = lcs_noisy_adu / (aux_data['sint'] * integration_time_s)
    lcs_noisy_mag = mr.irradiance_to_apparent_magnitude(lcs_noisy_irrad)
    var_lcs = np.var(lcs_noisy_mag, axis=0)
    mean_lcs = np.mean(lcs_noisy_mag, axis=0)

    plt.plot(epsecs, mean_lcs, c='k', lw=1)
    for stdev in [1, 2, 3]:
        plt.fill_between(
            epsecs,
            np.clip(mean_lcs - (stdev - 1) * np.sqrt(var_lcs), 0, np.inf),
            np.clip(mean_lcs - stdev * np.sqrt(var_lcs), 0, np.inf),
            alpha=0.4 - 0.1 * stdev,
            color='b',
            edgecolor=None,
        )
        plt.fill_between(
            epsecs,
            np.clip(mean_lcs + (stdev - 1) * np.sqrt(var_lcs), 0, np.inf),
            np.clip(mean_lcs + stdev * np.sqrt(var_lcs), 0, np.inf),
            alpha=0.4 - 0.1 * stdev,
            color='b',
            edgecolor=None,
        )
    mrv.texit(
        this_dates[0].strftime('%Y-%m-%d'),
        '',
        '',
        grid=False,
        legend=['Mean', '1$\sigma$', '2$\sigma$', '3$\sigma$'] if nights == 0 else None,
    )
    plt.ylim(13, 18)
    plt.gca().invert_yaxis()

plt.gcf().supxlabel('Seconds after midnight UTC')
plt.gcf().supylabel('Recieved irradiance [W/m$^2$]')

plt.tight_layout()
plt.show()

/Users/liamrobinson/Documents/maintained-research/mirage/examples/01-light_curves/lc_uncertainty.py:146: SyntaxWarning: invalid escape sequence '\s'
  legend=['Mean', '1$\sigma$', '2$\sigma$', '3$\sigma$'] if nights == 0 else None,
/Users/liamrobinson/Documents/maintained-research/mirage/examples/01-light_curves/lc_uncertainty.py:146: SyntaxWarning: invalid escape sequence '\s'
  legend=['Mean', '1$\sigma$', '2$\sigma$', '3$\sigma$'] if nights == 0 else None,
/Users/liamrobinson/Documents/maintained-research/mirage/examples/01-light_curves/lc_uncertainty.py:146: SyntaxWarning: invalid escape sequence '\s'
  legend=['Mean', '1$\sigma$', '2$\sigma$', '3$\sigma$'] if nights == 0 else None,
WARNING: no observation constraints assigned!
40702.22889884547
/Users/liamrobinson/Documents/maintained-research/mirage/.venv/lib/python3.12/site-packages/numpy/core/_methods.py:173: RuntimeWarning: invalid value encountered in subtract
  x = asanyarray(arr - arrmean)
WARNING: no observation constraints assigned!
40630.120822650046
WARNING: no observation constraints assigned!
40573.89948136731
WARNING: no observation constraints assigned!
52444.95496296702