Neural Network Brightness

Trains a neural network to predict the brightness of a specular cube in an arbitrary lighting and observation conditions and compares the results to the truth

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

import mirage as mr
import mirage.sim as mrsim

Let’s define the object and the BRDF

obj = mr.SpaceObject('cube.obj')
brdf = mr.Brdf('phong', cd=0.5, cs=0.5, n=10)

We now define the Multi-Layer Perceptron (MLP) brightness model. Note that the layers=(150, 50, 150) keyword argument defines the number of neurons in each densely-connected layer.

mlp_bm = mrsim.MLPBrightnessModel(obj, brdf, use_engine=False)

Now we train the model on a set number of training lighting and observation configurations. Usually 1e5-1e6 are required for a good fit

num_train = int(1e3)
mlp_bm.train(num_train)

Compute training LC: 4.17e-03 seconds
Iteration 1, loss = 0.18127016
Iteration 2, loss = 0.15971763
Iteration 3, loss = 0.14518729
Iteration 4, loss = 0.14468459
Iteration 5, loss = 0.14270959
Iteration 6, loss = 0.14034678
Iteration 7, loss = 0.13924839
Iteration 8, loss = 0.13747428
Iteration 9, loss = 0.13568279
Iteration 10, loss = 0.13423521
Iteration 11, loss = 0.13228884
Iteration 12, loss = 0.13143481
Iteration 13, loss = 0.12912974
Iteration 14, loss = 0.12572225
Iteration 15, loss = 0.12449965
Iteration 16, loss = 0.12084617
Iteration 17, loss = 0.11743524
Iteration 18, loss = 0.11436193
Iteration 19, loss = 0.11396536
Iteration 20, loss = 0.10650785
Iteration 21, loss = 0.10136535
Iteration 22, loss = 0.09817745
Iteration 23, loss = 0.09346670
Iteration 24, loss = 0.08929212
Iteration 25, loss = 0.08710523
Iteration 26, loss = 0.07951026
Iteration 27, loss = 0.07382954
Iteration 28, loss = 0.06809999
Iteration 29, loss = 0.06485453
Iteration 30, loss = 0.06470504
Iteration 31, loss = 0.05722733
Iteration 32, loss = 0.05328395
Iteration 33, loss = 0.05192525
Iteration 34, loss = 0.04699091
Iteration 35, loss = 0.04654311
Iteration 36, loss = 0.04572273
Iteration 37, loss = 0.04176225
Iteration 38, loss = 0.03886622
Iteration 39, loss = 0.03732021
Iteration 40, loss = 0.03708705
Iteration 41, loss = 0.03665159
Iteration 42, loss = 0.03506733
Iteration 43, loss = 0.03929847
Iteration 44, loss = 0.03287851
Iteration 45, loss = 0.02944032
Iteration 46, loss = 0.02918808
Iteration 47, loss = 0.02964126
Iteration 48, loss = 0.03331463
Iteration 49, loss = 0.02639978
Iteration 50, loss = 0.02446701
Iteration 51, loss = 0.02304622
Iteration 52, loss = 0.02230175
Iteration 53, loss = 0.02259354
Iteration 54, loss = 0.02095502
Iteration 55, loss = 0.02183407
Iteration 56, loss = 0.02136469
Iteration 57, loss = 0.02071164
Iteration 58, loss = 0.01841063
Iteration 59, loss = 0.01830396
Iteration 60, loss = 0.01775726
Iteration 61, loss = 0.01635375
Iteration 62, loss = 0.01524434
Iteration 63, loss = 0.01628099
Iteration 64, loss = 0.01649877
Iteration 65, loss = 0.01480635
Iteration 66, loss = 0.01370462
Iteration 67, loss = 0.01331505
Iteration 68, loss = 0.01374542
Iteration 69, loss = 0.01361906
Iteration 70, loss = 0.01311694
Iteration 71, loss = 0.01286734
Iteration 72, loss = 0.01249137
Iteration 73, loss = 0.01145654
Iteration 74, loss = 0.01082221
Iteration 75, loss = 0.00990209
Iteration 76, loss = 0.00954866
Iteration 77, loss = 0.01094308
Iteration 78, loss = 0.01070894
Iteration 79, loss = 0.00973992
Iteration 80, loss = 0.00959623
Iteration 81, loss = 0.01018976
Iteration 82, loss = 0.00909165
Iteration 83, loss = 0.00990398
Iteration 84, loss = 0.00866342
Iteration 85, loss = 0.00851127
Iteration 86, loss = 0.00777333
Iteration 87, loss = 0.00844034
Iteration 88, loss = 0.00802195
Iteration 89, loss = 0.00749687
Iteration 90, loss = 0.00685436
Iteration 91, loss = 0.00698969
Iteration 92, loss = 0.00716177
Iteration 93, loss = 0.00670340
Iteration 94, loss = 0.00705420
Iteration 95, loss = 0.00646013
Iteration 96, loss = 0.00557650
Iteration 97, loss = 0.00568275
Iteration 98, loss = 0.00527456
Iteration 99, loss = 0.00525986
Iteration 100, loss = 0.00564726
Iteration 101, loss = 0.00518418
Iteration 102, loss = 0.00519960
Iteration 103, loss = 0.00525598
Iteration 104, loss = 0.00538686
Iteration 105, loss = 0.00577426
Iteration 106, loss = 0.00531530
Iteration 107, loss = 0.00528764
Iteration 108, loss = 0.00502740
Iteration 109, loss = 0.00468601
Iteration 110, loss = 0.00452877
Iteration 111, loss = 0.00393577
Iteration 112, loss = 0.00420734
Iteration 113, loss = 0.00377504
Iteration 114, loss = 0.00395416
Iteration 115, loss = 0.00365817
Iteration 116, loss = 0.00355717
Iteration 117, loss = 0.00320249
Iteration 118, loss = 0.00317987
Iteration 119, loss = 0.00354016
Iteration 120, loss = 0.00381158
Iteration 121, loss = 0.00327871
Iteration 122, loss = 0.00304621
Iteration 123, loss = 0.00307948
Iteration 124, loss = 0.00288133
Iteration 125, loss = 0.00271460
Iteration 126, loss = 0.00278249
Iteration 127, loss = 0.00307248
Iteration 128, loss = 0.00288129
Iteration 129, loss = 0.00264396
Iteration 130, loss = 0.00277377
Iteration 131, loss = 0.00260349
Iteration 132, loss = 0.00256791
Iteration 133, loss = 0.00251144
Iteration 134, loss = 0.00268363
Iteration 135, loss = 0.00257028
Iteration 136, loss = 0.00235136
Iteration 137, loss = 0.00221710
Iteration 138, loss = 0.00212835
Iteration 139, loss = 0.00222850
Iteration 140, loss = 0.00203674
Iteration 141, loss = 0.00200141
Iteration 142, loss = 0.00209581
Iteration 143, loss = 0.00201188
Iteration 144, loss = 0.00221775
Iteration 145, loss = 0.00191832
Iteration 146, loss = 0.00188845
Iteration 147, loss = 0.00193473
Iteration 148, loss = 0.00184473
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
Fit against 1000 pts: : 1.45e+00 seconds

We can now simulate a torque-free attitude profile to inspect the quality of the fit

t_eval = np.linspace(0, 10, 1000)
q, _ = mr.propagate_attitude_torque_free(
    np.array([0.0, 0.0, 0.0, 1.0]),
    np.array([1.0, 1.0, 1.0]),
    np.diag([1, 2, 3]),
    t_eval,
)
dcm = mr.quat_to_dcm(q)
ovb = mr.stack_mat_mult_vec(dcm, np.array([[1, 0, 0]]))
svb = mr.stack_mat_mult_vec(dcm, np.array([[0, 1, 0]]))

Evaluating the model in its two available formats - as a native scikit-learn model and as an Open Neural Network eXchange (ONNX) model

mr.tic('Evaluate trained model with sklearn')
mdl_b_sklearn = mlp_bm.eval(ovb, svb, eval_mode_pref='sklearn')
mr.toc()
mr.tic('Evaluate trained model with onnx')
mdl_b_onnx = mlp_bm.eval(ovb, svb, eval_mode_pref='onnx')
mr.toc()

Evaluate trained model with sklearn: 5.17e-03 seconds
Evaluate trained model with onnx: 5.75e-03 seconds

We can save both of these representations to file:

mlp_bm.save_to_file(save_as_format='onnx')
mlp_bm.save_to_file(save_as_format='sklearn')

Now we load the model from its .onxx file we just saved and evaluate the brightness

mlp_bm.load_from_file(mlp_bm.onnx_file_name)
mr.tic('Evaluate loaded model with onxx')
mdl_onnx_loaded = mlp_bm.eval(ovb, svb, eval_mode_pref='onnx')
mr.toc()

Evaluate loaded model with onxx: 9.89e-04 seconds

And we do the same for the scikit-learn .plk file we saved

mlp_bm.load_from_file(mlp_bm.sklearn_file_name)
mr.tic('Evaluate loaded model with sklearn')
mdl_sklearn_loaded = mlp_bm.eval(ovb, svb, eval_mode_pref='sklearn')
mr.toc()

Evaluate loaded model with sklearn: 1.75e-02 seconds

We can easily confirm that all four model evaluations have produced the same prediction

print(np.max(np.abs(mdl_b_sklearn - mdl_onnx_loaded)))
print(np.max(np.abs(mdl_b_onnx - mdl_onnx_loaded)))
print(np.max(np.abs(mdl_b_sklearn - mdl_sklearn_loaded)))
print(np.max(np.abs(mdl_b_onnx - mdl_sklearn_loaded)))

1.1904903565174152e-06
0.0
0.0
1.1904903565174152e-06

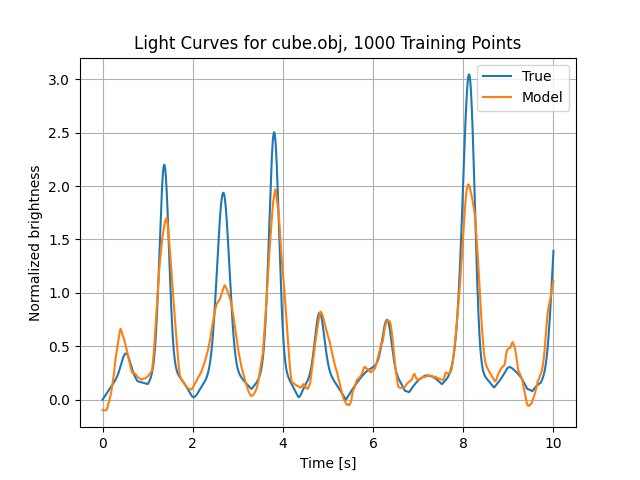
We can now finish off by evaluating the true brightness in this attitude profile and plot the results

true_b = mlp_bm.brightness(svb, ovb)

plt.figure()
sns.lineplot(x=t_eval, y=true_b, errorbar=None)
sns.lineplot(x=t_eval, y=mdl_b_sklearn, errorbar=None)
plt.title(f'Light Curves for {obj.file_name}, {num_train} Training Points')
plt.xlabel('Time [s]')
plt.ylabel('Normalized brightness')
plt.legend(['True', 'Model'])
plt.grid()
plt.show()

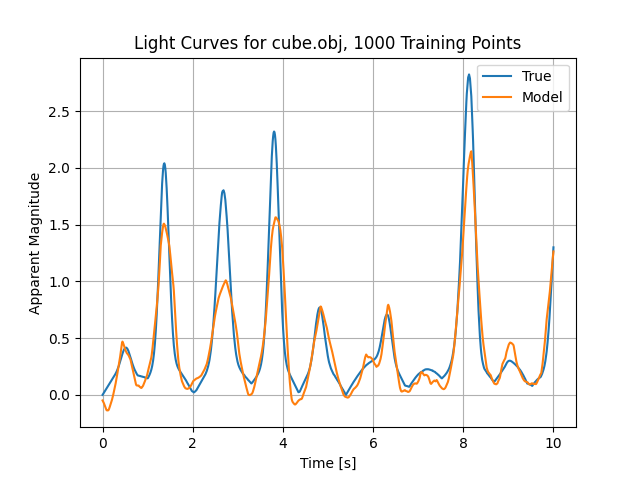
We can also train on magnitude data instead of irradiance:

mlp_bm = mrsim.MLPBrightnessModel(obj, brdf, use_engine=True)
mlp_bm.train(num_train)

mr.tic('Evaluate trained model with onnx')
mdl_b_onnx = mlp_bm.eval(ovb, svb)
mr.toc()

Compute training LC: 4.32e-01 seconds
Iteration 1, loss = 0.15383222
Iteration 2, loss = 0.12860092
Iteration 3, loss = 0.12190140
Iteration 4, loss = 0.12034833
Iteration 5, loss = 0.11891312
Iteration 6, loss = 0.11650769
Iteration 7, loss = 0.11574559
Iteration 8, loss = 0.11311555
Iteration 9, loss = 0.11082573
Iteration 10, loss = 0.10949464
Iteration 11, loss = 0.10819203
Iteration 12, loss = 0.10552360
Iteration 13, loss = 0.10323249
Iteration 14, loss = 0.10138305
Iteration 15, loss = 0.09836298
Iteration 16, loss = 0.09556053
Iteration 17, loss = 0.09292782
Iteration 18, loss = 0.08964601
Iteration 19, loss = 0.08652054
Iteration 20, loss = 0.08268762
Iteration 21, loss = 0.07977501
Iteration 22, loss = 0.08228252
Iteration 23, loss = 0.07679573
Iteration 24, loss = 0.06967056
Iteration 25, loss = 0.06369299
Iteration 26, loss = 0.05897063
Iteration 27, loss = 0.05647592
Iteration 28, loss = 0.05378805
Iteration 29, loss = 0.05173586
Iteration 30, loss = 0.04826785
Iteration 31, loss = 0.04564298
Iteration 32, loss = 0.04311183
Iteration 33, loss = 0.04189250
Iteration 34, loss = 0.03922629
Iteration 35, loss = 0.03945175
Iteration 36, loss = 0.03783237
Iteration 37, loss = 0.03394205
Iteration 38, loss = 0.03382036
Iteration 39, loss = 0.03187589
Iteration 40, loss = 0.03317893
Iteration 41, loss = 0.03038195
Iteration 42, loss = 0.02918105
Iteration 43, loss = 0.02823664
Iteration 44, loss = 0.02696648
Iteration 45, loss = 0.02536136
Iteration 46, loss = 0.02451248
Iteration 47, loss = 0.02351191
Iteration 48, loss = 0.02445325
Iteration 49, loss = 0.02216246
Iteration 50, loss = 0.02313051
Iteration 51, loss = 0.02074650
Iteration 52, loss = 0.02117626
Iteration 53, loss = 0.01993771
Iteration 54, loss = 0.01925369
Iteration 55, loss = 0.01887440
Iteration 56, loss = 0.01738671
Iteration 57, loss = 0.01776394
Iteration 58, loss = 0.01561698
Iteration 59, loss = 0.01561775
Iteration 60, loss = 0.01536234
Iteration 61, loss = 0.01405181
Iteration 62, loss = 0.01402327
Iteration 63, loss = 0.01350892
Iteration 64, loss = 0.01325144
Iteration 65, loss = 0.01291480
Iteration 66, loss = 0.01287152
Iteration 67, loss = 0.01213826
Iteration 68, loss = 0.01253371
Iteration 69, loss = 0.01240384
Iteration 70, loss = 0.01163455
Iteration 71, loss = 0.01129040
Iteration 72, loss = 0.01189344
Iteration 73, loss = 0.01062586
Iteration 74, loss = 0.01034234
Iteration 75, loss = 0.00995148
Iteration 76, loss = 0.00976747
Iteration 77, loss = 0.00906219
Iteration 78, loss = 0.00881076
Iteration 79, loss = 0.00843662
Iteration 80, loss = 0.00869331
Iteration 81, loss = 0.00910649
Iteration 82, loss = 0.00814298
Iteration 83, loss = 0.00781486
Iteration 84, loss = 0.00728303
Iteration 85, loss = 0.00753384
Iteration 86, loss = 0.00725868
Iteration 87, loss = 0.00705023
Iteration 88, loss = 0.00653763
Iteration 89, loss = 0.00676153
Iteration 90, loss = 0.00799113
Iteration 91, loss = 0.00780466
Iteration 92, loss = 0.00791341
Iteration 93, loss = 0.00702701
Iteration 94, loss = 0.00648043
Iteration 95, loss = 0.00621494
Iteration 96, loss = 0.00562588
Iteration 97, loss = 0.00544263
Iteration 98, loss = 0.00632153
Iteration 99, loss = 0.00517282
Iteration 100, loss = 0.00524577
Iteration 101, loss = 0.00518609
Iteration 102, loss = 0.00500562
Iteration 103, loss = 0.00496355
Iteration 104, loss = 0.00517992
Iteration 105, loss = 0.00460269
Iteration 106, loss = 0.00460374
Iteration 107, loss = 0.00433101
Iteration 108, loss = 0.00436360
Iteration 109, loss = 0.00461320
Iteration 110, loss = 0.00427921
Iteration 111, loss = 0.00404413
Iteration 112, loss = 0.00378767
Iteration 113, loss = 0.00360761
Iteration 114, loss = 0.00387193
Iteration 115, loss = 0.00458863
Iteration 116, loss = 0.00422199
Iteration 117, loss = 0.00386618
Iteration 118, loss = 0.00369868
Iteration 119, loss = 0.00349830
Iteration 120, loss = 0.00392715
Iteration 121, loss = 0.00343952
Iteration 122, loss = 0.00302652
Iteration 123, loss = 0.00309288
Iteration 124, loss = 0.00350759
Iteration 125, loss = 0.00307144
Iteration 126, loss = 0.00300187
Iteration 127, loss = 0.00276320
Iteration 128, loss = 0.00293399
Iteration 129, loss = 0.00271292
Iteration 130, loss = 0.00267208
Iteration 131, loss = 0.00268750
Iteration 132, loss = 0.00249051
Iteration 133, loss = 0.00263747
Iteration 134, loss = 0.00242556
Iteration 135, loss = 0.00255347
Iteration 136, loss = 0.00275226
Iteration 137, loss = 0.00254509
Iteration 138, loss = 0.00244953
Iteration 139, loss = 0.00225946
Iteration 140, loss = 0.00234673
Iteration 141, loss = 0.00206780
Iteration 142, loss = 0.00200022
Iteration 143, loss = 0.00220398
Iteration 144, loss = 0.00195489
Iteration 145, loss = 0.00202366
Iteration 146, loss = 0.00185070
Iteration 147, loss = 0.00186922
Iteration 148, loss = 0.00187552
Iteration 149, loss = 0.00183205
Iteration 150, loss = 0.00184794
Iteration 151, loss = 0.00205505
Iteration 152, loss = 0.00191610
Iteration 153, loss = 0.00206417
Iteration 154, loss = 0.00180324
Iteration 155, loss = 0.00183520
Iteration 156, loss = 0.00187315
Iteration 157, loss = 0.00161133
Iteration 158, loss = 0.00150517
Iteration 159, loss = 0.00155981
Iteration 160, loss = 0.00152109
Iteration 161, loss = 0.00163661
Iteration 162, loss = 0.00153717
Iteration 163, loss = 0.00142755
Iteration 164, loss = 0.00134956
Iteration 165, loss = 0.00133207
Iteration 166, loss = 0.00130611
Iteration 167, loss = 0.00139266
Iteration 168, loss = 0.00152360
Iteration 169, loss = 0.00155982
Training loss did not improve more than tol=0.000100 for 10 consecutive epochs. Stopping.
Fit against 1000 pts: : 4.57e+00 seconds
Evaluate trained model with onnx: 1.75e-02 seconds

We can now finish off by evaluating the true brightness in this attitude profile and plot the results

true_b = mlp_bm.brightness(svb, ovb)

plt.figure()
sns.lineplot(x=t_eval, y=true_b, errorbar=None)
sns.lineplot(x=t_eval, y=mdl_b_onnx, errorbar=None)
plt.title(f'Light Curves for {obj.file_name}, {num_train} Training Points')
plt.xlabel('Time [s]')
plt.ylabel('Apparent Magnitude')
plt.legend(['True', 'Model'])
plt.grid()
plt.show()