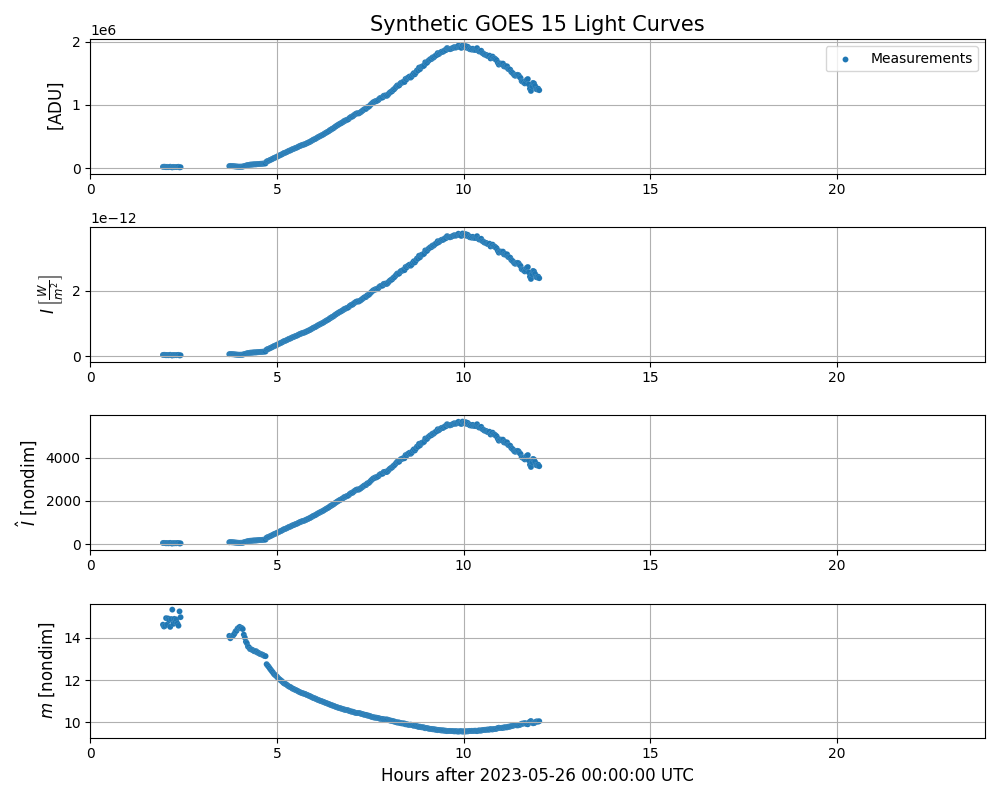
Light Curve Units

Expressing the same light curve in different units.

import datetime
from typing import Any

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

import mirage as mr
import mirage.vis as mrv


def aligned_nadir_constrained_sun_attitude(
    obj: mr.SpaceObject, dates: np.ndarray[datetime.datetime, Any]
) -> mr.AlignedAndConstrainedAttitude:
    r_obj_j2k = obj.propagate(dates)
    sv = mr.sun(dates)
    nadir = -mr.hat(r_obj_j2k)
    return mr.AlignedAndConstrainedAttitude(
        v_align=nadir, v_const=sv, dates=dates, axis_order=(1, 2, 0)
    )

Setting up analysis times

date_start = mr.utc(2023, 5, 26)
(dates, epsecs) = mr.date_arange(
    date_start - mr.days(1), date_start, mr.seconds(100), return_epsecs=True
)
ephr = epsecs / 3600  # Epoch hours
integration_time_s = 10.0  # Seconds

Setting up the scenario objects

obj = mr.SpaceObject('matlib_hylas4.obj', identifier='goes 15')
brdf = mr.Brdf('phong')
station = mr.Station(preset='pogs')
# Observing from the Purdue Optical Ground Station in New Mexico

Model file matlib_hylas4.obj not found in current model folder ('/Users/liamrobinson/Documents/maintained-research/mirage/mirage/resources/models'), checking model repository...
Attempting to download matlib_hylas4.obj and its associated material file from the model repository...
Requesting: https://raw.githubusercontent.com/ljrobins/mirage-models/main//accurate_sats/matlib_hylas4.obj
Model files were downloaded successfully!

Defining observation constraints on the station

station.constraints = [
    mr.SnrConstraint(3),
    mr.ElevationConstraint(10),
    mr.TargetIlluminatedConstraint(),
    mr.ObserverEclipseConstraint(station),
    mr.VisualMagnitudeConstraint(18),
    mr.MoonExclusionConstraint(30),
]

Defining the object’s attitude profile and mass properties

obj_attitude = aligned_nadir_constrained_sun_attitude(obj, dates)

Computing the full noisy light curve

(lc_noisy_sampler, aux_data) = station.observe_light_curve(
    obj,
    obj_attitude,
    brdf,
    dates,
    integration_time_s,
    use_engine=True,
    model_scale_factor=1,
    show_window=True,
    instances=1,
    rotate_panels=True,
)
lc_noisy = lc_noisy_sampler()

2025-02-26 22:42:52.639 LightCurveEngine-mac-arm[39838:1419874] +[IMKClient subclass]: chose IMKClient_Modern
2025-02-26 22:42:52.639 LightCurveEngine-mac-arm[39838:1419874] +[IMKInputSession subclass]: chose IMKInputSession_Modern

Extracting data and plotting results

lc_clean = aux_data['lc_clean']
sint = aux_data['sint']

plt.figure(figsize=(10, 8))
plt.subplot(4, 1, 1)
sns.scatterplot(x=ephr, y=lc_noisy, linewidth=0.05, size=0.1)
# sns.scatterplot(x=ephr, y=lc_clean, linewidth=0.05, size=0.05, color="k")
plt.xlim((0, np.max(ephr)))
mrv.texit(
    'Synthetic GOES 15 Light Curves',
    '',
    r'$\left[\mathrm{ADU} \right]$',
    ['Measurements'],
)

lc_noisy_irrad = lc_noisy / (sint * integration_time_s)
lc_clean_irrad = lc_clean / (sint * integration_time_s)
plt.subplot(4, 1, 2)
sns.scatterplot(x=ephr, y=lc_noisy_irrad, linewidth=0.05, size=0.2)
# sns.scatterplot(x=ephr, y=lc_clean_irrad, linewidth=0.05, size=0.1, color="k")
mrv.texit(
    '',
    '',
    r'$I \: \left[ \frac{W}{m^2} \right]$',
)
plt.xlim((0, np.max(ephr)))

lc_noisy_irrad_unit = lc_noisy_irrad * (aux_data['rmag_station_to_sat'] * 1e3) ** 2
lc_clean_irrad_unit = lc_clean_irrad * (aux_data['rmag_station_to_sat'] * 1e3) ** 2
plt.subplot(4, 1, 3)
sns.scatterplot(x=ephr, y=lc_noisy_irrad_unit, linewidth=0.05, size=0.2)
# sns.scatterplot(x=ephr, y=lc_clean_irrad_unit, linewidth=0.05, size=0.1, color="k")
mrv.texit(
    '',
    '',
    r'$\hat{I}$ [nondim]',
)
plt.xlim((0, np.max(ephr)))

lc_noisy_mag = mr.irradiance_to_apparent_magnitude(lc_noisy_irrad)
lc_clean_mag = mr.irradiance_to_apparent_magnitude(lc_clean_irrad)
plt.subplot(4, 1, 4)
sns.scatterplot(x=ephr, y=lc_noisy_mag, linewidth=0.05, size=0.05)
# sns.scatterplot(x=ephr, y=lc_clean_mag, linewidth=0.05, size=0.1, color="k")
mrv.texit(
    '',
    f'Hours after {date_start.strftime("%Y-%m-%d %H:%M:%S UTC")}',
    '$m$ [nondim]',
)
plt.xlim((0, np.max(ephr)))
plt.tight_layout()
plt.show()