Coordinate System Interpolation

Interpolating the transformation between two coordinate systems.

import matplotlib.pyplot as plt
import numpy as np

import mirage as mr

station = mr.Station()

dates, epsecs = mr.date_linspace(
    mr.now(), mr.now() + mr.hours(24), 1_00, return_epsecs=True
)
fine_dates, fine_epsecs = mr.date_linspace(
    dates[0], dates[-1], dates.size * 10, return_epsecs=True
)
interpolator = mr.FrameInterpolator('j2000', 'itrf', dates, max_surface_error_km=1e-4)

mr.tic('Computing rotation matrices')
dcms = mr.EarthFixedFrame('j2000', 'itrf').rotms_at_dates(dates)
mr.toc()

mr.tic('Computing rotation matrices, fine')
dcms_fine = mr.EarthFixedFrame('j2000', 'itrf').rotms_at_dates(fine_dates)
mr.toc()

mr.tic('Evaluate interpolator')
fine_dcms_interp = interpolator(fine_epsecs)
mr.toc()

Computing rotation matrices: 4.93e-03 seconds
Computing rotation matrices, fine: 3.40e-02 seconds
Evaluate interpolator: 1.44e-04 seconds

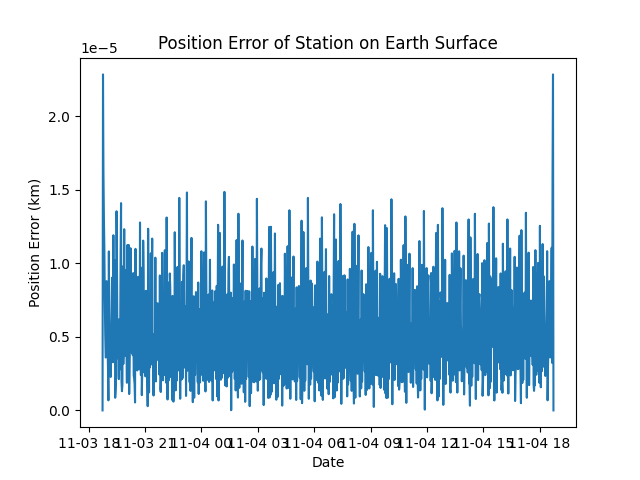
Comparing with true values, via the error in the position of a station on the surface

pos_err_interp = (
    mr.stack_mat_mult_vec(fine_dcms_interp, station.j2000_at_dates(fine_dates))
    - station.itrf
)

mean_pos_err = np.mean(mr.vecnorm(pos_err_interp))
max_pos_err = np.max(mr.vecnorm(pos_err_interp))
print(f'Mean position error: {mean_pos_err} km')
print(f'Max position error: {max_pos_err} km')

Mean position error: 5.389894337664337e-06 km
Max position error: 2.2836176246252774e-05 km

Plotting

plt.figure()
plt.plot(fine_dates, mr.vecnorm(pos_err_interp))
plt.xlabel('Date')
plt.ylabel('Position Error (km)')
plt.title('Position Error of Station on Earth Surface')
plt.show()

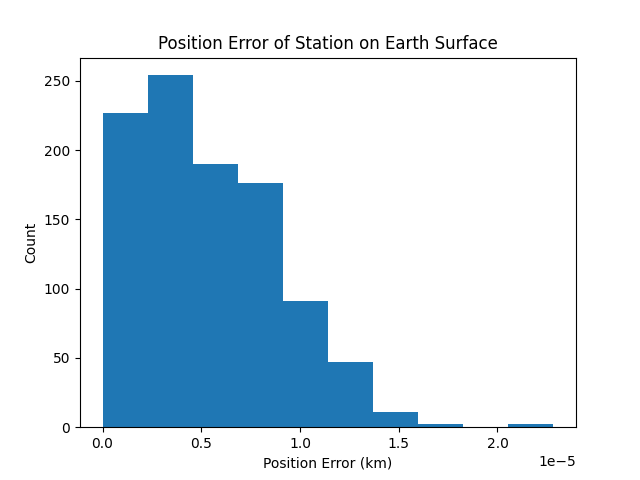
plt.figure()
plt.hist(mr.vecnorm(pos_err_interp))
plt.ylabel('Count')
plt.xlabel('Position Error (km)')
plt.title('Position Error of Station on Earth Surface')
plt.show()

• 
•