PRNG Speed

Benchmarking the speed of various numpy pseudorandom number generators

from timeit import timeit

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from numba import njit

import mirage as mr

n = 4096**2  # the number of pixels in our CCD image
mus = np.random.randint(100, 100000, size=n).reshape(-1, 16)

Poisson PRNG

names = ['MT19937', 'MT19937', 'PCG64', 'PCG64DXSM', 'Philox', 'SFC64']
gens = [np.random.Generator(getattr(np.random, n)()).poisson for n in names]
gens.append(mr.multithreaded_poisson)
names.append('SFC64 8 threads')

data = {'dt': [], 'name': []}
for i, (gen, name) in enumerate(zip(gens, names)):
    mr.tic()
    samples = gen(mus)
    dt = mr.toc(return_elapsed_seconds=True)
    if i > 0:
        data['dt'].append(dt)
        data['name'].append(name)


g = sns.catplot(
    data=pd.DataFrame(data),
    kind='bar',
    x='name',
    y='dt',
    errorbar='sd',
    alpha=0.6,
    height=6,
)
g.despine(left=True)
g.set_axis_labels('', 'Time to sample image [s]')
g.legend.set_title('')
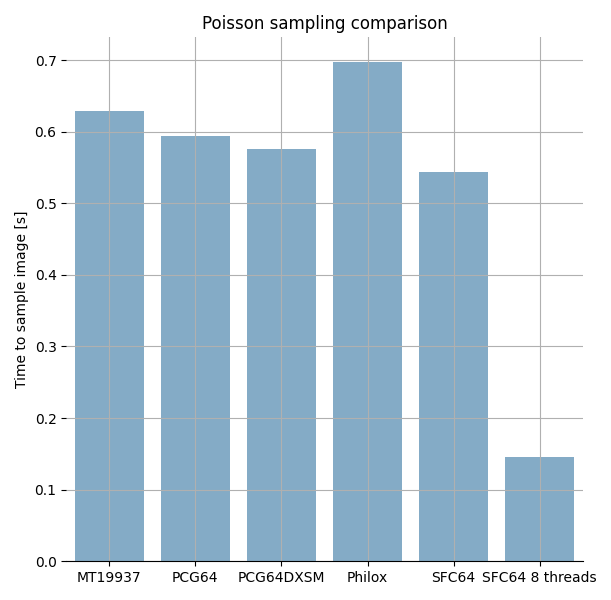
plt.title('Poisson sampling comparison')
plt.grid()
g.despine(left=True)
plt.tight_layout()
plt.show()

Gaussian PRNG

mus = np.random.randn(n).reshape(-1, 16)
sigmas = np.abs(np.random.randn(n).reshape(-1, 16))

names = ['MT19937', 'MT19937', 'PCG64', 'PCG64DXSM', 'Philox', 'SFC64']
gens = [np.random.Generator(getattr(np.random, n)()).normal for n in names]
gens.append(mr.multithreaded_gaussian)
names.append('SFC64 8 threads')

data = {'dt': [], 'name': []}
for i, (gen, name) in enumerate(zip(gens, names)):
    mr.tic()
    samples = gen(mus, sigmas)
    dt = mr.toc(return_elapsed_seconds=True)
    if i > 0:
        data['dt'].append(dt)
        data['name'].append(name)

g = sns.catplot(
    data=pd.DataFrame(data),
    kind='bar',
    x='name',
    y='dt',
    errorbar='sd',
    alpha=0.6,
    height=6,
)
g.set_axis_labels('', 'Time to sample image [s]')
g.legend.set_title('')
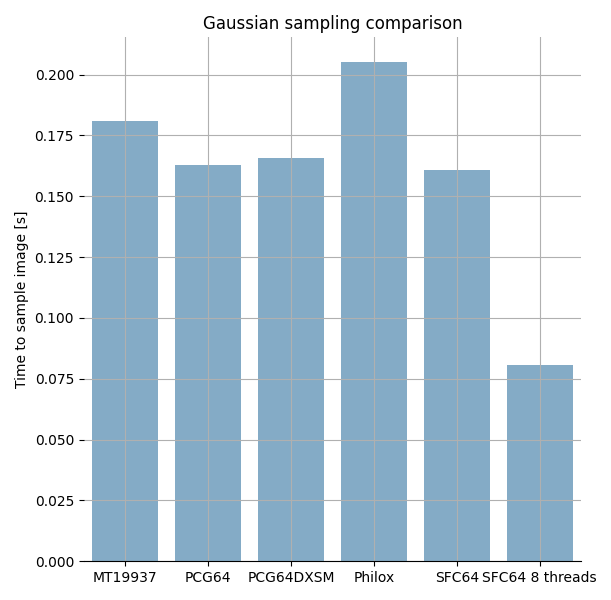
plt.title('Gaussian sampling comparison')
plt.grid()
g.despine(left=True)
plt.tight_layout()
plt.show()

Numba for sampling normals faster

bit_gen = np.random.SFC64()
next_d = bit_gen.cffi.next_double
state_addr = bit_gen.cffi.state_address


@njit
def normals_numba(n, state):
    out = np.empty(n)
    for i in range((n + 1) // 2):
        x1 = 2.0 * next_d(state) - 1.0
        x2 = 2.0 * next_d(state) - 1.0
        r2 = x1 * x1 + x2 * x2
        while r2 >= 1.0 or r2 == 0.0:
            x1 = 2.0 * next_d(state) - 1.0
            x2 = 2.0 * next_d(state) - 1.0
            r2 = x1 * x1 + x2 * x2
        f = np.sqrt(-2.0 * np.log(r2) / r2)
        out[2 * i] = f * x1
        if 2 * i + 1 < n:
            out[2 * i + 1] = f * x2
    return out


n = 4096**2


def numbacall():
    return normals_numba(n, state_addr)


rg = np.random.Generator(bit_gen)


def numpycall():
    return rg.normal(size=n)


# Check that the functions work
r1 = numbacall()
r2 = numpycall()
assert r1.shape == (n,)
assert r1.shape == r2.shape

t1 = timeit(numbacall, number=3)
print(f'{t1:.2f} secs for {n} PCG64 (Numba/SFC64) gaussian randoms')
t2 = timeit(numpycall, number=3)
print(f'{t2:.2f} secs for {n} PCG64 (NumPy/SFC64) gaussian randoms')

0.81 secs for 16777216 PCG64 (Numba/SFC64) gaussian randoms
0.22 secs for 16777216 PCG64 (NumPy/SFC64) gaussian randoms