Atmospheric Refraction

Computing the effect of atmospheric refraction on observations

True elevation: 55.7 deg
Apparent elevation: 55.71173209771628 deg
Refraction: 42.23555177859453 arcsec

import matplotlib.pyplot as plt
import numpy as np

import mirage as mr
import mirage.vis as mrv

true_el = np.deg2rad(np.linspace(15.1, 90, int(1e3)))
atmos_pressure = 1028.4463393  # mbar
atmos_temp = 277.594  # Kelvin

apparent_el = mr.apparent_refacted_elevation(atmos_pressure, atmos_temp, true_el)

test_el_deg = 55.7
test_el_rad = np.deg2rad(test_el_deg)
app_el_deg = np.rad2deg(
    mr.apparent_refacted_elevation(atmos_pressure, atmos_temp, test_el_rad)
)
delta_el_deg = app_el_deg - test_el_deg
delta_el_arcsec = delta_el_deg * 3600
print(f'True elevation: {test_el_deg} deg')
print(f'Apparent elevation: {app_el_deg} deg')
print(f'Refraction: {delta_el_arcsec} arcsec')

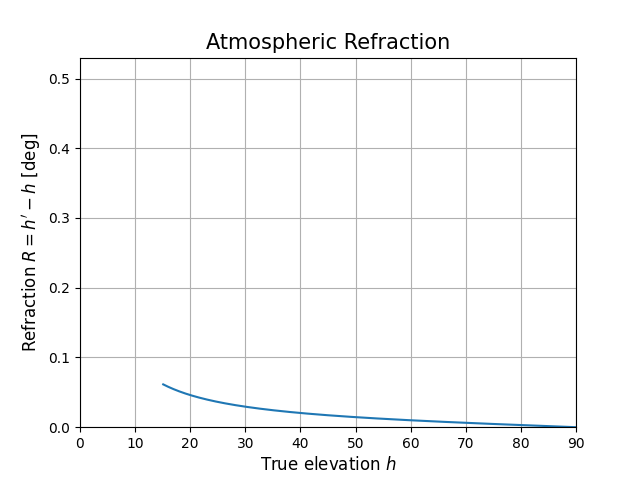
plt.plot(np.rad2deg(true_el), np.rad2deg(apparent_el - true_el))
mrv.texit(
    'Atmospheric Refraction', 'True elevation $h$', "Refraction $R = h' - h$ [deg]"
)
plt.xlim(0, 90)
plt.ylim(0, 0.53)
plt.show()