Atmospheric Scintillation

Quantifying the noise atmospheric turbulence introduces into photometry :cite:p:osborn2015:.

0.0015556032055347526
mad_percent=0.12411917804316258
0.0015556442870763019

import matplotlib.pyplot as plt
import numpy as np

import mirage as mr

station = mr.Station()

t = 3  # Exposure time in seconds
H = 8e3  # Scaleheight of the atmospheric turbulence, this is the generally accepted value
theta_z = 0.68  # Zenith angle
factor_of_safety = 1.5

sigmay = station.scintillation_noise_std(theta_z, t, factor_of_safety=factor_of_safety)
print(sigmay)

mad_percent = np.sqrt(2 / np.pi) * sigmay * 100
print(f'{mad_percent=}')

x = np.random.normal(1, scale=sigmay, size=int(1e7))
print(sigma_y_num := np.sqrt((np.mean(x**2) - x.mean() ** 2) / x.mean() ** 2))
plt.hist((x - 1) * 100, bins=100, density=True)
prev_ylim = plt.ylim()
plt.vlines(
    np.array([-3 * sigmay, 3 * sigmay]) * 100,
    *prev_ylim,
    colors='k',
    label='$\pm 3 \sigma$',
)
plt.ylim(*prev_ylim)
plt.xlabel('Percent intensity deviation')
plt.ylabel('Probability density')
plt.grid()
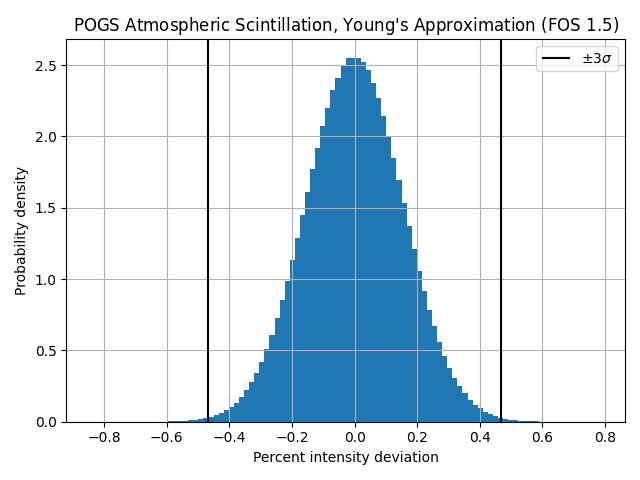
plt.title(
    f"POGS Atmospheric Scintillation, Young's Approximation (FOS ${factor_of_safety}$)"
)
plt.legend()
plt.tight_layout()
plt.show()