Self-Shadowing Methods

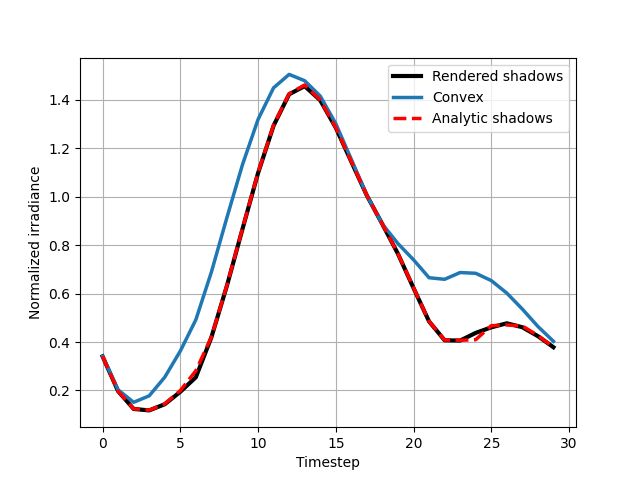
Comparing light curves produced by different shadowing methods

shape: (10_000, 11)
┌───────┬───────────┬───────────────┬───────────────┬───┬───────┬─────────────────────┬─────────────────────┬─────────────────────┐
│ index ┆ fun       ┆ xk            ┆ x0            ┆ … ┆ geval ┆ gradient            ┆ hessian_inverse     ┆ lcs                 │
│ ---   ┆ ---       ┆ ---           ┆ ---           ┆   ┆ ---   ┆ ---                 ┆ ---                 ┆ ---                 │
│ u32   ┆ f32       ┆ array[f32, 6] ┆ array[f32, 6] ┆   ┆ i32   ┆ array[f32, 6]       ┆ array[f32, (6, 6)]  ┆ array[f32, 30]      │
╞═══════╪═══════════╪═══════════════╪═══════════════╪═══╪═══════╪═════════════════════╪═════════════════════╪═════════════════════╡
│ 9516  ┆ 0.003955  ┆ [-0.390662,   ┆ [-0.854759,   ┆ … ┆ 61    ┆ [0.000745,          ┆ [[0.081833,         ┆ [1.007337,          │
│       ┆           ┆ -0.119828, …  ┆ -0.391406, …  ┆   ┆       ┆ 0.007497, …         ┆ -0.030074, … 0.002… ┆ 1.161327, …         │
│       ┆           ┆ -2.79…        ┆ -1.31…        ┆   ┆       ┆ -0.0027…            ┆                     ┆ 0.71495…            │
│ 7848  ┆ 0.003957  ┆ [-0.387673,   ┆ [-0.75457,    ┆ … ┆ 52    ┆ [0.000419,          ┆ [[0.47441,          ┆ [1.007049,          │
│       ┆           ┆ -0.120137, …  ┆ -0.105496, …  ┆   ┆       ┆ -0.029104, …        ┆ -0.090327, …        ┆ 1.159802, …         │
│       ┆           ┆ -2.80…        ┆ -2.300…       ┆   ┆       ┆ -0.012…             ┆ -0.350…             ┆ 0.71338…            │
│ 5107  ┆ 0.003969  ┆ [-0.394871,   ┆ [-0.13018,    ┆ … ┆ 87    ┆ [0.000559,          ┆ [[0.008096,         ┆ [1.006594,          │
│       ┆           ┆ -0.119215, …  ┆ -0.418386, …  ┆   ┆       ┆ -0.002142, …        ┆ -0.002591, … -0.00… ┆ 1.162603, …         │
│       ┆           ┆ -2.79…        ┆ -0.718…       ┆   ┆       ┆ 0.0033…             ┆                     ┆ 0.71686…            │
│ 3030  ┆ 0.00397   ┆ [-0.387203,   ┆ [-0.225484,   ┆ … ┆ 64    ┆ [-0.036694,         ┆ [[0.883299,         ┆ [1.008699,          │
│       ┆           ┆ -0.120736, …  ┆ 0.262925, …   ┆   ┆       ┆ -0.14035, … -0.023… ┆ -0.272552, … -0.47… ┆ 1.161966, …         │
│       ┆           ┆ -2.80…        ┆ -2.329…       ┆   ┆       ┆                     ┆                     ┆ 0.71283…            │
│ 9284  ┆ 0.003988  ┆ [-0.394471,   ┆ [-0.568772,   ┆ … ┆ 102   ┆ [-0.005588,         ┆ [[0.030263,         ┆ [1.007527,          │
│       ┆           ┆ -0.119497, …  ┆ -0.512208, …  ┆   ┆       ┆ -0.017975, … -0.00… ┆ -0.011778, … 0.051… ┆ 1.163444, …         │
│       ┆           ┆ -2.79…        ┆ -1.34…        ┆   ┆       ┆                     ┆                     ┆ 0.71716…            │
│ …     ┆ …         ┆ …             ┆ …             ┆ … ┆ …     ┆ …                   ┆ …                   ┆ …                   │
│ 3251  ┆ 21.450222 ┆ [-0.450625,   ┆ [0.264644,    ┆ … ┆ 10    ┆ [672.531128,        ┆ [[0.541913,         ┆ [1.106782, 1.0612,  │
│       ┆           ┆ -0.40518, …   ┆ 0.17325, …    ┆   ┆       ┆ 1688.194336, … 13…  ┆ -0.347993, … -0.34… ┆ … 0.611774]         │
│       ┆           ┆ 0.2182…       ┆ 0.468316…     ┆   ┆       ┆                     ┆                     ┆                     │
│ 9342  ┆ 22.012674 ┆ [-0.736319,   ┆ [-0.736319,   ┆ … ┆ 10    ┆ [1545.333862,       ┆ [[1.0, 0.0, … 0.0], ┆ [0.773308,          │
│       ┆           ┆ -0.56701, …   ┆ -0.56701, …   ┆   ┆       ┆ 41.007996, … 15.…   ┆ [0.0, 1.0,…         ┆ 0.742228, …         │
│       ┆           ┆ -0.056…       ┆ -0.056…       ┆   ┆       ┆                     ┆                     ┆ 0.58402…            │
│ 8171  ┆ 22.586926 ┆ [0.574946,    ┆ [0.574915,    ┆ … ┆ 7     ┆ [10612.106445,      ┆ [[0.979192,         ┆ [1.792547,          │
│       ┆           ┆ 0.587646, …   ┆ 0.587201, …   ┆   ┆       ┆ 9823.608398, … …    ┆ -0.1572, … -0.1962… ┆ 1.827346, …         │
│       ┆           ┆ 1.79112…      ┆ 1.79055…      ┆   ┆       ┆                     ┆                     ┆ 0.56664…            │
│ 2350  ┆ 25.570591 ┆ [-0.052748,   ┆ [-0.087239,   ┆ … ┆ 9     ┆ [5152.320801,       ┆ [[0.4907,           ┆ [1.918925,          │
│       ┆           ┆ -0.218768, …  ┆ -0.244219, …  ┆   ┆       ┆ 2141.380371, … 4…   ┆ -0.563388, …        ┆ 2.054583, …         │
│       ┆           ┆ -0.02…        ┆ -0.04…        ┆   ┆       ┆                     ┆ -0.5067…            ┆ 0.44642…            │
│ 3003  ┆ 27.241659 ┆ [0.474602,    ┆ [0.474528,    ┆ … ┆ 12    ┆ [4146.766602,       ┆ [[0.911092,         ┆ [0.411008,          │
│       ┆           ┆ -0.138677, …  ┆ -0.138728, …  ┆   ┆       ┆ 6980.705566, … 9…   ┆ -0.160831, … -0.10… ┆ 0.451678, …         │
│       ┆           ┆ -1.127…       ┆ -1.127…       ┆   ┆       ┆                     ┆                     ┆ 1.73245…            │
└───────┴───────────┴───────────────┴───────────────┴───┴───────┴─────────────────────┴─────────────────────┴─────────────────────┘
2024-11-03 13:40:16.490 LightCurveEngine-mac-arm[23844:2256213] +[IMKClient subclass]: chose IMKClient_Modern
2024-11-03 13:40:16.490 LightCurveEngine-mac-arm[23844:2256213] +[IMKInputSession subclass]: chose IMKInputSession_Modern

import os

import matplotlib.pyplot as plt
import numpy as np
import polars as pl

import mirage as mr

mr.set_model_directory(
    '/Users/liamrobinson/Documents/maintained-research/mirage-models/Non-Convex/'
)
obj = mr.SpaceObject('irregular.obj')

brdf = mr.Brdf('blinn-phong', cd=0.5, cs=0.5, n=5.0)
df = pl.read_parquet(os.path.join(os.environ['SRCDIR'], '..', 'saved.parquet'))
print(df)
x0 = np.array([0.0, 0.0, 0.0, -3.0, 3.0, 1.0])
lc = [
    0.341383,
    0.197364,
    0.123992,
    0.118558,
    0.144448,
    0.199170,
    0.281262,
    0.420311,
    0.634635,
    0.868985,
    1.099806,
    1.296503,
    1.425755,
    1.462219,
    1.400128,
    1.286364,
    1.145995,
    1.006063,
    0.886744,
    0.765302,
    0.624586,
    0.485581,
    0.408199,
    0.407272,
    0.409617,
    0.467555,
    0.470402,
    0.466237,
    0.426641,
    0.379301,
]

itensor = np.diag([1.0, 2.0, 3.0])
t = np.linspace(0, 1, len(lc), endpoint=False)
svi = np.tile(np.array([1.0, 0.0, 0.0]), (len(t), 1))
ovi = np.tile(np.array([np.sqrt(2) / 2, np.sqrt(2) / 2, 0.0]), (len(t), 1))
# ovi = np.array([np.cos(t), np.sin(t), 0.0*t]).T

s0 = x0[:3]
w0 = x0[3:]

attitude = mr.RbtfAttitude(w0, mr.mrp_to_quat(s0), itensor)
q_of_t, _ = attitude.propagate(t)
c_of_t = mr.quat_to_dcm(q_of_t)
svb = mr.stack_mat_mult_vec(c_of_t, svi)
ovb = mr.stack_mat_mult_vec(c_of_t, ovi)

lc_engine = mr.run_light_curve_engine(
    brdf, obj, svb, ovb, show_window=True, instances=1, frame_rate=40
)
lc_convex = obj.convex_light_curve(brdf, svb, ovb)

plt.plot(lc_engine, 'k', linewidth=3, label='Rendered shadows')
plt.plot(lc_convex, linewidth=2.5, label='Convex')
plt.plot(lc, 'r--', linewidth=2.5, label='Analytic shadows')
plt.grid()
plt.xlabel('Timestep')
plt.ylabel('Normalized irradiance')
plt.legend()
plt.show()