Note
Go to the end to download the full example code.
Importance Sampling#
Reducing the variance of Monte Carlo integration
import matplotlib.pyplot as plt
import numpy as np
import sympy as sp
from scipy.stats.sampling import TransformedDensityRejection
Let’s say we want to estimate the integral of an unknown function \(f(x)\)
x = sp.symbols('x')
f_symbolic = sp.sin(np.pi * x)
bounds = (0, 1)
f = sp.lambdify(x, f_symbolic)
xs = np.linspace(*bounds, 1000)
plt.plot(xs, f(xs))
plt.grid()
plt.title('f(x)')
plt.xlabel('x')
plt.show()
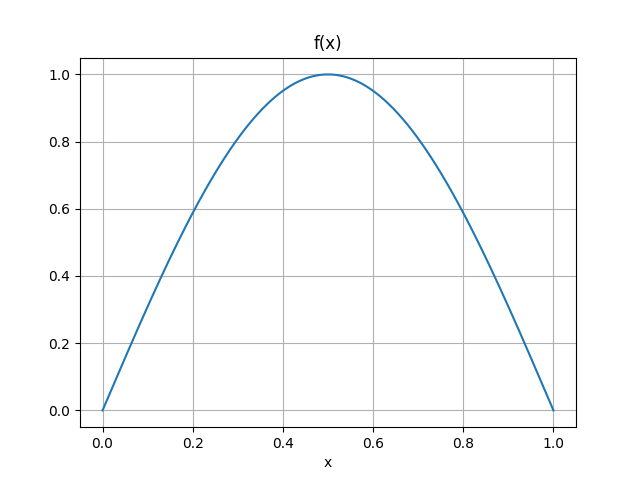
We can analytically compute the integral of this function
int_symbolic = sp.integrate(f_symbolic, (x, 0, 1))
print(f'The analytic integral is {int_symbolic:.4f}')
The analytic integral is 0.6366
A naive attempt at Monte Carlo integration would be to uniformly take samples of the function over the integral and average them
n = 10 # number of samples
f_of_x_naive = f(np.random.rand(n))
int_naive = f_of_x_naive.sum() / n
percent_error_naive = (int_naive - int_symbolic) / int_symbolic * 100
print(
f'The naive Monte Carlo integral is {int_naive:.4f}, {percent_error_naive:.2f}% error'
)
The naive Monte Carlo integral is 0.4992, -21.58% error
The fundamental idea of importance sampling is that our Monte Carlo result will be better if we take samples from a distribution that looks like the true function, dividing each sample by its pdf likelihood. To accomplish this, let’s select a pdf that might help
class NewPdf:
def pdf(self, x: float) -> float:
# Note that this is slightly
return -6 * x**2 + 6 * x
def dpdf(self, x: float) -> float:
return -12 * x + 6
dist = NewPdf()
pdf = TransformedDensityRejection(
dist, random_state=np.random.default_rng(), domain=[0, 1]
)
Let’s try Monte Carlo integration again with the new pdf
xs_sample = pdf.rvs(n)
int_importance = (f(xs_sample) / dist.pdf(xs_sample)).sum() / n
percent_error_importance = (int_importance - int_symbolic) / int_symbolic * 100
print(
f'The importance sampled integral is {int_importance:.4f}, {percent_error_importance:.2f}% error'
)
The importance sampled integral is 0.6347, -0.29% error
Let’s take a look at the points we sampled
true_pdf = f(xs) / int_symbolic
plt.figure()
plt.plot(xs, true_pdf)
plt.plot(xs, dist.pdf(xs))
plt.scatter(xs_sample, 0 * xs_sample, s=5, alpha=0.2)
plt.grid()
plt.title('probability')
plt.xlabel('x')
plt.legend(['true pdf', 'approximate pdf', 'samples'])
plt.show()
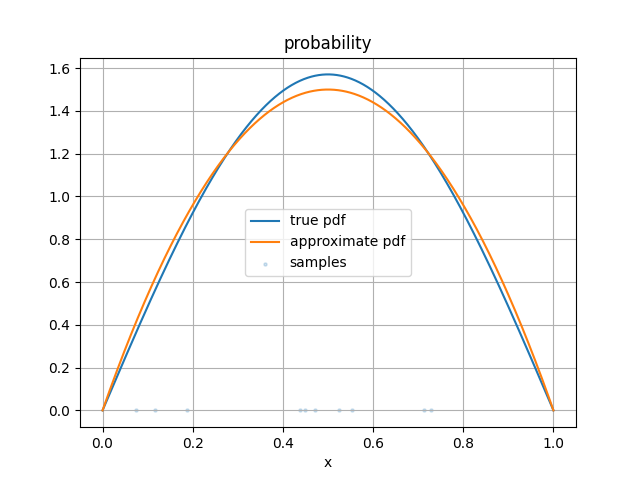
Total running time of the script: (0 minutes 1.472 seconds)
