Torque-free Attitude Propagation

Comparing various methods for propagating torque-free rigid-body motion

import matplotlib.pyplot as plt
import numpy as np

import mirage as mr
import mirage.vis as mrv

itensor = np.diag([1.0, 1.0, 2.0])

num_time, num_ic = 10, 10
ntime = np.logspace(0, 1.0, num_time, dtype=np.int32) + 1
nic = np.logspace(0, 1.0, num_ic, dtype=np.int32)
nt_grid, ni_grid = np.meshgrid(ntime, nic)

w0s = mr.rand_unit_vectors(max(nic))
q0s = mr.rand_quaternions(max(nic))

nt, ni = int(1e6), int(1e1)
q0 = mr.rand_quaternions(ni)
w0 = mr.rand_unit_vectors(ni)
mr.tic()
q_par, _ = mr.propagate_attitude_torque_free_axisymmetric(
    q0, w0, itensor, np.linspace(0, 1, nt)
)
dt = mr.toc(return_elapsed_seconds=True)
print(f'Axisymmetric form: {nt * ni / dt:.2e} [quats/sec]')

mr.tic()
q_ana, _ = mr.propagate_attitude_torque_free(
    q0[0, :], w0[0, :], itensor, np.linspace(0, 1, nt)
)
dt = mr.toc(return_elapsed_seconds=True)
print(f'Generalized form: {nt * 1 / dt:.2e} [quats/sec]')

err = np.max(
    np.abs(mr.quat_upper_hemisphere(q_ana) - mr.quat_upper_hemisphere(q_par[0, :, :]))
)
print(f'Max quaternion error: {err}')

Axisymmetric form: 7.81e+06 [quats/sec]
Generalized form: 7.99e+06 [quats/sec]
Max quaternion error: 0.0

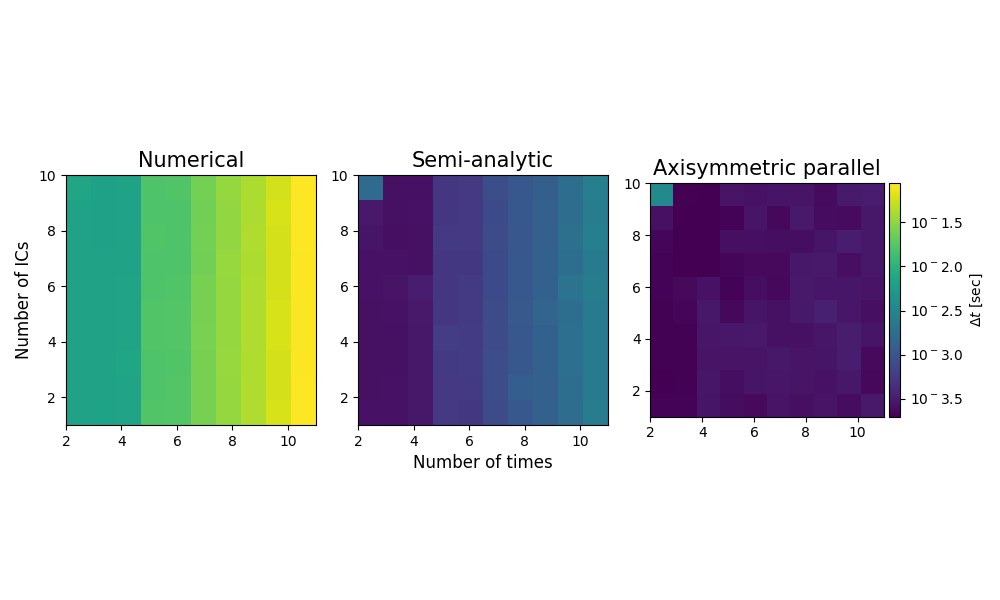
Let’s test a whole grid of options to stress test these methods

t_axi = np.zeros_like(nt_grid, dtype=np.float64)
t_ana = np.zeros_like(nt_grid, dtype=np.float64)
t_num = np.zeros_like(nt_grid, dtype=np.float64)
for k, (ni, nt) in enumerate(zip(ni_grid.flatten(), nt_grid.flatten())):
    i, j = k // num_time, k % num_time
    q0, w0 = q0s[:ni, :], w0s[:ni, :]
    tspace = np.linspace(0, 1, nt)
    mr.tic()
    q_par = mr.propagate_attitude_torque_free_axisymmetric(q0, w0, itensor, tspace)
    t_axi[i, j] = mr.toc(return_elapsed_seconds=True)
    mr.tic()
    for q, w in zip(q0, w0):
        q_true1, _ = mr.propagate_attitude_torque_free(q, w, itensor, tspace)
    t_ana[i, j] = mr.toc(return_elapsed_seconds=True)
    mr.tic()
    for q, w in zip(q0, w0):
        q_true2, _ = mr.integrate_rigid_attitude_dynamics(q, w, itensor, tspace)
    t_num[i, j] = mr.toc(return_elapsed_seconds=True)

allt = np.log10(np.concatenate([t_num, t_ana, t_axi]).flatten())
tlims = np.min(allt), np.max(allt)
titles = ['Numerical', 'Semi-analytic', 'Axisymmetric parallel']
plt.figure(figsize=(10, 6))
for i, grid in enumerate([t_num, t_ana, t_axi], 1):
    plt.subplot(1, 3, i)
    plt.imshow(
        np.log10(grid).T,
        vmin=tlims[0],
        vmax=tlims[1],
        extent=(np.min(ntime), np.max(ntime), np.min(nic), np.max(nic)),
    )
    mrv.texit(
        titles[i - 1],
        'Number of times' if i == 2 else None,
        'Number of ICs' if i == 1 else None,
        grid=False,
    )
    if i == 3:
        cb = plt.colorbar(label='$\Delta t$ [sec]', cax=mrv.get_cbar_ax())
        tics = cb.get_ticks()
        cb.set_ticklabels([f'$10^{t}$' for t in tics])
    plt.tight_layout()
plt.show()

/Users/liamrobinson/Documents/maintained-research/mirage/examples/06-attitude/torque_free_axisymmetric.py:87: SyntaxWarning: invalid escape sequence '\D'
  cb = plt.colorbar(label='$\Delta t$ [sec]', cax=mrv.get_cbar_ax())
/Users/liamrobinson/Documents/maintained-research/mirage/examples/06-attitude/torque_free_axisymmetric.py:89: UserWarning: set_ticklabels() should only be used with a fixed number of ticks, i.e. after set_ticks() or using a FixedLocator.
  cb.set_ticklabels([f'$10^{t}$' for t in tics])