Third Body Interpolation

Interpolating the position of a third body for more efficient propagation with low error.

import matplotlib.pyplot as plt

import mirage as mr

target_body = ('jupiter', mr.jupiter)

Define a date range and a set of points to interpolate

npts = int(1e2)
dates, epsecs = mr.date_linspace(
    mr.now(),
    mr.now() + mr.days(mr.AstroConstants.moon_sidereal_period_days),
    npts,
    return_epsecs=True,
)
pts = target_body[1](dates)
fine_dates, fine_epsecs = mr.date_linspace(
    dates[0], dates[-1], dates.size * 10, return_epsecs=True
)

Building an interpolator

mr.tic('Building interpolator')
interpolator = mr.SpiceInterpolator(target_body[0], dates)
mr.toc()
mr.tic('Interpolating')
pts_interp = interpolator(fine_epsecs)
mr.toc()
mr.tic('Computing true positions')
pts_fine_true = target_body[1](fine_dates)
mr.toc()

Building interpolator: 2.36e-03 seconds
Interpolating: 5.13e-05 seconds
Computing true positions: 1.59e-02 seconds

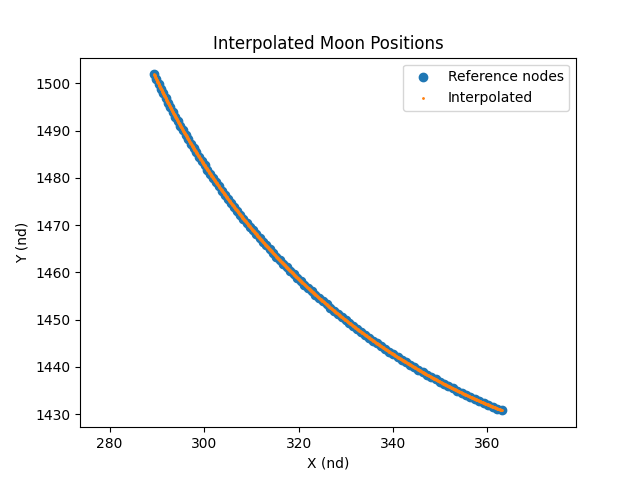
Plot the interpolated points

pts_nd = pts / mr.AstroConstants.moon_orbit_semimajor_axis
pts_interp_nd = pts_interp / mr.AstroConstants.moon_orbit_semimajor_axis
plt.figure()
plt.scatter(pts_nd[:, 0], pts_nd[:, 1], label='Reference nodes')
plt.scatter(pts_interp_nd[:, 0], pts_interp_nd[:, 1], s=1, label='Interpolated')
plt.axis('equal')
plt.title('Interpolated Moon Positions')
plt.xlabel('X (nd)')
plt.ylabel('Y (nd)')
plt.legend()

<matplotlib.legend.Legend object at 0x31b091340>

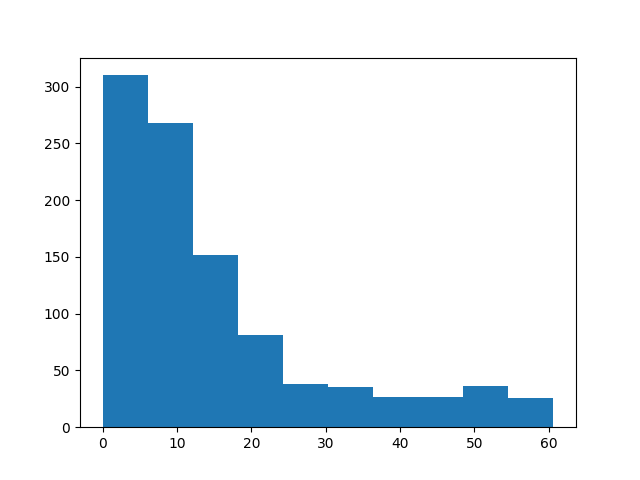
Computing the error of the interpolation

plt.figure()
pts_error = pts_interp - pts_fine_true
pts_error_norm = mr.vecnorm(pts_error)
plt.hist(pts_error_norm)
plt.show()