Quaternion Sampling Efficiency

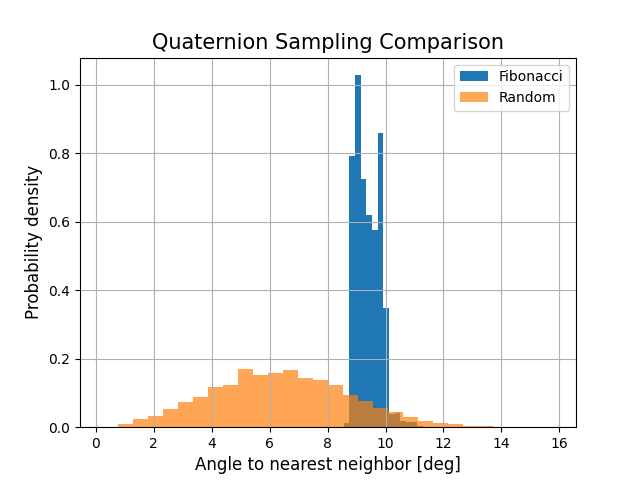
Comparing methods for sampling quaternions, with an emphasis on distributing the quaternions uniformly throughout orientation space (in the cosine distance sense)

import matplotlib.pyplot as plt
import numpy as np
# from sklearn.neighbors import BallTree
from pykdtree.kdtree import KDTree
from scipy.stats import norm
from scipy.stats.qmc import Halton
from smt.sampling_methods import LHS

import mirage as mr
import mirage.vis as mrv

n = int(1e3)
np.random.seed(1)

Q = mr.quat_upper_hemisphere(mr.quaternion_fibonacci_sample(n))
cq = KDTree(Q).query(Q, k=2)[1][:, 1]

ang1 = mr.quat_ang(Q, Q[cq, :], deg=True)

Q = mr.quat_upper_hemisphere(mr.rand_quaternions(n))
cq = KDTree(Q).query(Q, k=2)[1][:, 1]
ang2 = mr.quat_ang(Q, Q[cq, :], deg=True)

sampler = Halton(d=4, seed=1)
quantiles = sampler.random(n)
Q = mr.quat_upper_hemisphere(mr.hat(norm(loc=0, scale=1).ppf(quantiles)))
cq = KDTree(Q).query(Q, k=2)[1][:, 1]
ang3 = mr.quat_ang(Q, Q[cq, :], deg=True)

sampler = LHS(xlimits=np.array(4 * [[0, 1]]), random_state=1)
quantiles = sampler(n)
Q = mr.quat_upper_hemisphere(mr.hat(norm(loc=0, scale=1).ppf(quantiles)))
cq = KDTree(Q).query(Q, k=2)[1][:, 1]
ang4 = mr.quat_ang(Q, Q[cq, :], deg=True)

plt.hist(ang2, bins=30, alpha=1.0, label='Random', density=True)
plt.hist(ang1, bins=30, alpha=0.5, label='Fibonacci', density=True)
plt.hist(ang3, bins=30, alpha=0.5, label='Halton', density=True)
plt.hist(ang4, bins=30, alpha=0.5, label='LHS', density=True)
mrv.texit(
    'Quaternion Sampling Comparison',
    'Angle to nearest neighbor [deg]',
    'Probability density',
)
plt.legend()
plt.show()